
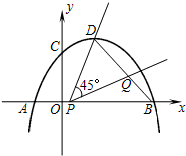 ШчЭМЃЌХзЮяЯп
ШчЭМЃЌХзЮяЯп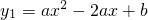 ЕФЖЅЕуЮЊDЃЌгыxжсНЛгкЕуAЃЌBЃЌгыyжсНЛгкЕуCЃЌЧвOB=2OC=3ЃЎ
ЕФЖЅЕуЮЊDЃЌгыxжсНЛгкЕуAЃЌBЃЌгыyжсНЛгкЕуCЃЌЧвOB=2OC=3ЃЎ DQЃЌЪдЧѓГіy2ЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ
DQЃЌЪдЧѓГіy2ЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛ ЗжБ№гыХзЮяЯпy1НЛгкЕуEЃЌGЃЌгыy2ЕФКЏЪ§ЭМЯѓНЛгкЕуFЃЌHЃЎЮЪЕуEЁЂFЁЂHЁЂGЮЇГЩЫФБпаЮЕФУцЛ§ФмЗёЮЊ
ЗжБ№гыХзЮяЯпy1НЛгкЕуEЃЌGЃЌгыy2ЕФКЏЪ§ЭМЯѓНЛгкЕуFЃЌHЃЎЮЪЕуEЁЂFЁЂHЁЂGЮЇГЩЫФБпаЮЕФУцЛ§ФмЗёЮЊ ЃПШєФмЃЌЧѓГіmЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєФмЃЌЧѓГіmЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ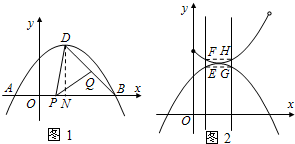 НтЃКЃЈ1ЃЉЁпOB=2ЃЌOC=
НтЃКЃЈ1ЃЉЁпOB=2ЃЌOC= ЃЌ
ЃЌ ЃЉСНЕуЃЌ
ЃЉСНЕуЃЌ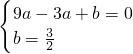 ЃЌ
ЃЌ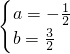
 x2+x+
x2+x+ ЃЎ
ЃЎ x2+x+
x2+x+ взЕУDЃЈ1ЃЌ2ЃЉЃЌNЃЈ1ЃЌ0ЃЉЃЌAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
взЕУDЃЈ1ЃЌ2ЃЉЃЌNЃЈ1ЃЌ0ЃЉЃЌAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ ЃЌ
ЃЌ ЃЉ2-22=PD2-ЃЈ1-xЃЉ2Ђй
ЃЉ2-22=PD2-ЃЈ1-xЃЉ2Ђй y2ЁС2
y2ЁС2 ЂкЃЎ
ЂкЃЎ x2-x+
x2-x+ ЃЎ
ЃЎ x2-x+
x2-x+ =
= ЃЈx-1ЃЉ2+2ЃЈ0ЁмxЃМ3ЃЉЃЎ
ЃЈx-1ЃЉ2+2ЃЈ0ЁмxЃМ3ЃЉЃЎ ЃЈШчЭМ2ЃЉ
ЃЈШчЭМ2ЃЉ x2+x+
x2+x+ =-
=- ЃЈx-1ЃЉ2+2ЃЈЗжБ№гыжБЯпx=mЃЌx=m+
ЃЈx-1ЃЉ2+2ЃЈЗжБ№гыжБЯпx=mЃЌx=m+ ЕФНЛЕу
ЕФНЛЕу ЃЈm-1ЃЉ2+2ЃЉЃЌGЃЈm+
ЃЈm-1ЃЉ2+2ЃЉЃЌGЃЈm+ ЃЌ-
ЃЌ- ЃЈm-1ЃЉ2+2ЃЉЃЎ
ЃЈm-1ЃЉ2+2ЃЉЃЎ ЃЈm-1ЃЉ2+2ЃЉЃЌHЃЈm+
ЃЈm-1ЃЉ2+2ЃЉЃЌHЃЈm+ ЃЌ-
ЃЌ- ЃЈm-
ЃЈm- ЃЉ2+2ЃЉЃЎ
ЃЉ2+2ЃЉЃЎ ЃЈm-1ЃЉ2+2-[-
ЃЈm-1ЃЉ2+2-[- ЃЈm-1ЃЉ2+2]=ЃЈm-1ЃЉ2
ЃЈm-1ЃЉ2+2]=ЃЈm-1ЃЉ2 ЃЈm-
ЃЈm- ЃЉ2+2-[-
ЃЉ2+2-[- ЃЈm-
ЃЈm- ЃЉ2+2]=ЃЈm-
ЃЉ2+2]=ЃЈm- ЃЉ2ЃЎ
ЃЉ2ЃЎ [ЃЈm-1ЃЉ2+ЃЈm-
[ЃЈm-1ЃЉ2+ЃЈm- ЃЉ2]ЁС
ЃЉ2]ЁС =
=
 Лђ
Лђ ЃЈЖМдк0ЁмxЁм3ФкЃЉ
ЃЈЖМдк0ЁмxЁм3ФкЃЉ Лђ
Лђ ЪБЃЌEЁЂFЁЂHЁЂGЮЇГЩЫФБпаЮЕФУцЛ§ЮЊ
ЪБЃЌEЁЂFЁЂHЁЂGЮЇГЩЫФБпаЮЕФУцЛ§ЮЊ ЃЎ
ЃЎ ЃЉСНЕуЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЕУЖўДЮКЏЪ§НтЮіЪНжаЕФЮДжЊЪ§ЕФжЕМДПЩШЗЖЈЦфНтЮіЪНЃЛ
ЃЉСНЕуЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЕУЖўДЮКЏЪ§НтЮіЪНжаЕФЮДжЊЪ§ЕФжЕМДПЩШЗЖЈЦфНтЮіЪНЃЛ ЃЌДгМйЩшГіЗЂЧѓЕУmЕФжЕОЭЫЕУїДцдкЃЌЗёдђОЭВЛДцдкЃЎ
ЃЌДгМйЩшГіЗЂЧѓЕУmЕФжЕОЭЫЕУїДцдкЃЌЗёдђОЭВЛДцдкЃЎ

 ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 1 | 2 |
 ЕуЃЎ
ЕуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 21ЁЂШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊAЃЈ1ЃЌ-4ЃЉЃЌЧвЙ§ЕуBЃЈ3ЃЌ0ЃЉЃЎ
21ЁЂШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊAЃЈ1ЃЌ-4ЃЉЃЌЧвЙ§ЕуBЃЈ3ЃЌ0ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЃЈ2013•КгФЯЃЉШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊPЃЈ-2ЃЌ2ЃЉЃЌгыyжсНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЎШєЦНвЦИУХзЮяЯпЪЙЦфЖЅЕуPбижБЯпвЦЖЏЕНЕуPЁфЃЈ2ЃЌ-2ЃЉЃЌЕуAЕФЖдгІЕуЮЊAЁфЃЌдђХзЮяЯпЩЯPAЖЮЩЈЙ§ЕФЧјгђЃЈвѕгАВПЗжЃЉЕФУцЛ§ЮЊ
ЃЈ2013•КгФЯЃЉШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊPЃЈ-2ЃЌ2ЃЉЃЌгыyжсНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЎШєЦНвЦИУХзЮяЯпЪЙЦфЖЅЕуPбижБЯпвЦЖЏЕНЕуPЁфЃЈ2ЃЌ-2ЃЉЃЌЕуAЕФЖдгІЕуЮЊAЁфЃЌдђХзЮяЯпЩЯPAЖЮЩЈЙ§ЕФЧјгђЃЈвѕгАВПЗжЃЉЕФУцЛ§ЮЊВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЃЈ2013•ЖыУМЩНЪаЖўФЃЃЉвбжЊЃЌШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЈ1ЃЌ-2ЃЉЃЌжБЯпy=kx+mгыХзЮяЯпНЛгкAЁЂBСНЕуЃЌЦфжаOA=3ЃЌBЕудкyжсЩЯЃЎЕуPЮЊЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЈЕуPгыЕуAЁЂBВЛжиКЯЃЉЃЌЙ§ЕуPЧвДЙжБгкxжсЕФжБЯпгыетЬѕХзЮяЯпНЛгкЕуEЃЎ
ЃЈ2013•ЖыУМЩНЪаЖўФЃЃЉвбжЊЃЌШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЈ1ЃЌ-2ЃЉЃЌжБЯпy=kx+mгыХзЮяЯпНЛгкAЁЂBСНЕуЃЌЦфжаOA=3ЃЌBЕудкyжсЩЯЃЎЕуPЮЊЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЈЕуPгыЕуAЁЂBВЛжиКЯЃЉЃЌЙ§ЕуPЧвДЙжБгкxжсЕФжБЯпгыетЬѕХзЮяЯпНЛгкЕуEЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЃЈ2013•ЖѕЖћЖрЫЙЃЉШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЈ-1ЃЌ-1ЃЉЃЌЧвОЙ§ЕуAЁЂЕуBКЭзјБъдЕуOЃЌЕуBЕФКсзјБъЮЊ-3ЃЎ
ЃЈ2013•ЖѕЖћЖрЫЙЃЉШчЭМЃЌХзЮяЯпЕФЖЅЕуЮЊCЃЈ-1ЃЌ-1ЃЉЃЌЧвОЙ§ЕуAЁЂЕуBКЭзјБъдЕуOЃЌЕуBЕФКсзјБъЮЊ-3ЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com