
 如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.
如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.分析 (1)先根据等腰三角形三线合一的性质证明∠ADC=90°,再根据有一组对边平行且相等证明四边形ADCE是平行四边形,所以四边形ADCE是矩形;
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
解答 证明:(1)∵在△ABC中,AB=AC,点D为边BC的中点,
∴BD=DC,∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD且AE=BD,
∴AE∥DC且AE=DC,
∴四边形ADCE是平行四边形,
又∠ADC=90°,
∴四边形ADCE是矩形;
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形;
理由是:∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴∠ACD=45°,
∵∠ADC=90°,
∴△ADC是等腰直角三角形,
∴AD=CD,
∴矩形ADCE是正方形.
点评 本题考查了平行四边形、矩形、正方形的性质和判定、等腰直角三角形的性质和判定、等腰三角形三线合一的性质,熟练掌握矩形和正方形的判定是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
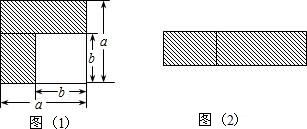
 如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )
如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )| A. | 12 | B. | 6+$\sqrt{6}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{6}$+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
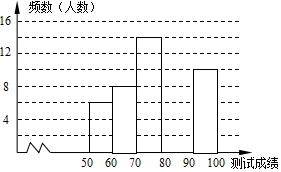 某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:
某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com