
����Ŀ����֪��������ABCD�ı߳�Ϊ![]() ���ף��Խ���AC�ϵ���������E,F����E�ӵ�A����F�ӵ�Cͬʱ�������ضԽ�����1����/�����ͬ�ٶ��˶�����E��EH��AC��Rt��ACD��ֱ�DZ���H����F��FG��AC��Rt��ACD��ֱ�DZ���G������HG��EB����HE��EF��FG��GHΧ�ɵ�ͼ�����Ϊ
���ף��Խ���AC�ϵ���������E,F����E�ӵ�A����F�ӵ�Cͬʱ�������ضԽ�����1����/�����ͬ�ٶ��˶�����E��EH��AC��Rt��ACD��ֱ�DZ���H����F��FG��AC��Rt��ACD��ֱ�DZ���G������HG��EB����HE��EF��FG��GHΧ�ɵ�ͼ�����Ϊ![]() ��AE��EB��BAΧ�ɵ�ͼ�����Ϊ
��AE��EB��BAΧ�ɵ�ͼ�����Ϊ![]() ������涨���߶ε����Ϊ
������涨���߶ε����Ϊ![]() ����E����C,F����Aֹͣ����E���˶�ʱ��Ϊx�룬����������⣺
����E����C,F����Aֹͣ����E���˶�ʱ��Ϊx�룬����������⣺
��1����ͼ�٣��ж��ı���EFGH��ʲô�ı��Σ���֤����
��2����0<x<8ʱ����xΪ��ֵʱ��![]() ��
��
��3����![]() ��
��![]() �ĺͣ�����x�Ĵ���ʽ��ʾy����ͼ��Ϊ����ͼ��
�ĺͣ�����x�Ĵ���ʽ��ʾy����ͼ��Ϊ����ͼ��


���𰸡���1���ı���EFGH�Ǿ��Σ�֤������������2��6����3��![]()
��������(1)�����ȸ��ݶ���E��F���˶��ٶ����˶�ʱ�����ͬ�ó�AE=CF�����������ε����ʼ���֪EH��AC��FG��AC�ó���CGF���AHE���ǵ���ֱ�������Σ�Ȼ�������һ������ֱ�ǵ�ƽ���ı����Ǿ��εó����ۣ�(2)�������ɹ��ɶ������������ABCD�ĶԽ��߳�Ϊ16��������BD��AC��O����BO=8��Ȼ���ú�x�Ĵ���ʽ�ֱ��ʾS1��S2����S1=S2ʱ�ó�����x�ķ��̣��ⷽ�̼��ɣ�(3)����Ϊ��x=8ʱ����E���F�غϣ���ʱS1=0��y=S2����Ӧ��0��x��8��8��x��16����������ۣ�
(1)���ı���EFGH�Ǿ��Σ�
֤������E��F�˶�ʱ����ͬ����AE=CF����![]() ��
��![]() ��
��![]() ��
��![]() ����EH//FG ��
����EH//FG ��
��ABCD��������AD=DC����D=900�����GCF=��HAE=450��
��![]() ��
��![]() ��
��![]() ��
��![]() �����CGF=��AHE=450�����GCF=��CGF����HAE=��AHE
�����CGF=��AHE=450�����GCF=��CGF����HAE=��AHE
��AE=EH��CF=FG����EH=FG �����ı���EFGH��ƽ���ı��Σ�
��![]() ��
��![]() �����ı���EFGH�Ǿ��Σ�
�����ı���EFGH�Ǿ��Σ�
(2)��![]() �����α߳�Ϊ
�����α߳�Ϊ![]() ��
��![]() ��
��
![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() �����
�����![]() ����ȥ����
����ȥ����![]() ��
�� ![]() ��
��![]() ʱ��
ʱ��![]() ��
��

(3)���ٵ�![]() ʱ��
ʱ��![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ��
��
![]() ��
�� ![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��1����x+2����x��3����x��x��4��������x=�� ![]()
��2����a+b����a��b��+��a+b��2��2a2 �� ����a=3��b=�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�����ֽƬ��һ��б�۹�ȥ������A����A�䴦��BCΪ�ۺۣ��ٽ�BE���۹�ȥ��BA���غϣ�BDΪ�ۺۣ���ô�����ۺ۵ļнǡ�CBD=�ȣ� 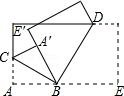
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�ܼƻ�ÿ������ij��Ʒ100�֣����ڹ���ʵ�����ݣ�ÿ���ϰ�������һ����ȣ�ʵ��ÿ����������ƻ������������±����Լƻ���Ϊ�������ӵĶ�����Ϊ���������ٵĶ�����Ϊ������
���� | һ | �� | �� | �� | �� | �� | �� |
����/�� | ��1 | +3 | ��2 | +4 | +7 | ��5 | ��10 |
��1������������һ������������ٵ�һ����������ٶ֣�
��2���������������Ƕ��ٶ֣���ԭ�ƻ������˻��Ǽ����ˣ�������Ϊ���ٶ֣�
��3���������������IJ�Ʒȫ����35������һ����װ�������뿪��������ƽ��ÿ��������Լ��װ�ض��ٶ֣��������ȷ��0.01�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ��������![]() ��ֱ�Ƕ���
��ֱ�Ƕ���![]() �ڵ�һ���ޣ�����
�ڵ�һ���ޣ�����![]() ��
��![]() �ֱ��ں���
�ֱ��ں���![]() ͼ���������֧�ϣ���
ͼ���������֧�ϣ���![]() ����ԭ��
����ԭ��![]() ��
��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ������
������![]() ����֪
����֪![]() ƽ���ı���
ƽ���ı���![]() �����.
�����.
(1)֤��:![]() :
:
(2)���![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�0��3������B��x���ϣ�����AOB�Ƶ�A��ʱ����ת90��õ���AEF����O��B�Ķ�Ӧ��ֱ��ǵ�E��F��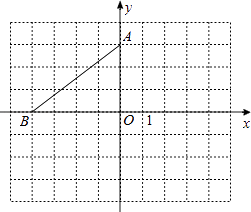
��1������B�������ǣ���4��0��������ͼ�л�����AEF����д����E��F�����꣮
��2������F����x����Ϸ�ʱ����д��һ�����������ĵ�B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ʵ������У�ij���̶ӽ���һ���ˮ���Ĺ��̣���������y���죩��ÿ����ɵĹ�����x��m/�죩�ĺ�����ϵͼ����ͼ��ʾ����˫���ߵ�һ���֣� 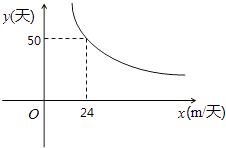
��1����������⣬��y��x֮��ĺ�������ʽ��
��2�����ù��̶���2̨�ھ����ÿ̨�ھ��ÿ���ܹ�����ˮ��15�ף��ʸù��̶����ö����������ɴ�������
��3�����Ϊ�˷�Ѵ�����Ľ�����Ҫ��������һ�����ڣ���30����㣩���������ôÿ������Ҫ��ɶ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͬѧ���в������ŷֱ�������� ![]() ��
�� ![]() ��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ����1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ����1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
��1������������ͼ���б����г����п��ܵĽ����
��2�����ƶ�����һ����Ϸ��������ѡ����a��b��ʹ��ax2+bx+1=0����������ȵ�ʵ��������Ƽ�ʤ��������һ�ʤ��������������Ϸ����ƽ�������ø���֪ʶ���ͣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com