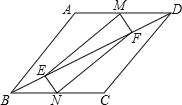
【题目】如图，已知平行四边形ABCD，点M，N分别在边AD和边BC上，点E，F在线段BD上，且AM=CN，DF=BE．求证：
（1）∠DFM=∠BEN；
（2）四边形MENF是平行四边形．
【答案】详见解析.
【解析】
试题分析：（1）由平行四边形的性质得到得AD∥BC，AD=BC，∠ADF=∠CBE，然后根据AM=CN得到DM=BN，从而证得△DMF≌△BNE，理由全等三角形对应角相等证得结论；（2）利用一组对边平行且相等的四边形为平行四边形进行判定即可．
试题解析：（1）由平行四边形ABCD得AD∥BC，AD=BC，∠ADF=∠CBE
∵AM=CN，
∴AD﹣AM=BC﹣CN，
即DM=BN，
又∵DF=BE，
∴△DMF≌△BNE，
∴∠DFM=∠BEN；
（2）由△DMF≌△BNE得NE=MF，
∵∠DFM=∠BEN得∠FEN=∠MFE，
∴MF∥NE，
∴四边形NEMF是平行四边形；
100分闯关期末冲刺系列答案科目：初中数学 来源： 题型：
【题目】在□ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连接EG、GF、FH、HE．
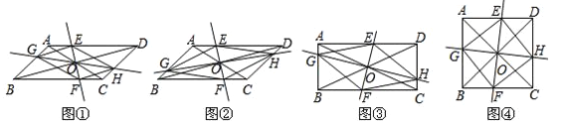
（1）如图①，试判断四边形EGFH的形状，并说明理由；
（2）如图②，当EF⊥GH时，四边形EGFH的形状是 ；
（3）如图③，在（2）的条件下，若AC=BD，四边形EGFH的形状是 ；
（4）如图④，在（3）的条件下，若AC⊥BD，试判断四边形EGFH的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
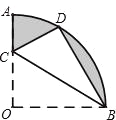
【题目】如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，则有下列选项：
①∠ACD=60°；
②CB=6
；
③阴影部分的周长为12+3π；
④阴影部分的面积为9π﹣12．
其中正确的是 （填写编号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等腰直角△ABC，∠A=90°．
（1）利用尺规作∠ABC的平分线BD，交AC于点D（保留作图痕迹，不写作法）；
（2）若将（1）中的△ABD沿BD折叠，则点A正好落在BC边上的A1处，当AB=1时，求△A1DC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间，设他从山脚出发后所用的时间为t(min)，所走的路程为s(m)，s与t之间的函数关系如图所示，请回答下列问题：
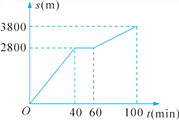
(1)小明中途休息用了几分钟？
(2)小明休息前爬山的平均速度为多少米每分钟？
(3)小明在上述过程中所走的路程为多少米？
(4)小明休息后爬山的平均速度为多少米每分钟？
查看答案和解析>>
科目：初中数学 来源： 题型：
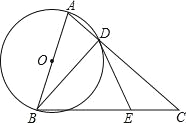
【题目】如图，在△ABC中，AC=BC，以AB为直径的⊙O交AC边于点D，点E在BC上，连结BD，DE，∠CDE=∠ABD．
（1）证明：DE是⊙O的切线；
（2）若BD=12，sin∠CDE=
，求圆O的半径和AC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
