
【题目】已知如图,矩形OABC的长OA= ![]() ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.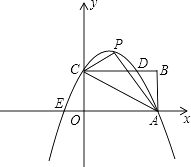
(1)求∠PCB的度数;
(2)若P,A两点在抛物线y=﹣ ![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
【答案】
(1)
解:在Rt△OAC中,OA= ![]() ,OC=1,则∠OAC=30°,∠OCA=60°;
,OC=1,则∠OAC=30°,∠OCA=60°;
根据折叠的性质知:OA=AP= ![]() ,∠ACO=∠ACP=60°;
,∠ACO=∠ACP=60°;
∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°.
(2)
解:过P作PQ⊥OA于Q;
Rt△PAQ中,∠PAQ=60°,AP= ![]() ;
;
∴OQ=AQ= ![]() ,PQ=
,PQ= ![]() ,
,
所以P( ![]() ,
, ![]() );
);
将P、A代入抛物线的解析式中,得:
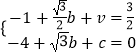 ,
,
解得 ![]() ;
;
即y=﹣ ![]() x2+
x2+ ![]() x+1;
x+1;
当x=0时,y=1,故C(0,1)在抛物线的图像上
(3)
解:①若DE是平行四边形的对角线,点C在y轴上,CD平行x轴,
∴过点D作DM∥CE交x轴于M,则四边形EMDC为平行四边形,
把y=1代入抛物线解析式得点D的坐标为( ![]() ,1)
,1)
把y=0代入抛物线解析式得点E的坐标为(﹣ ![]() ,0)
,0)
∴M( ![]() ,0);N点即为C点,坐标是(0,1);
,0);N点即为C点,坐标是(0,1);
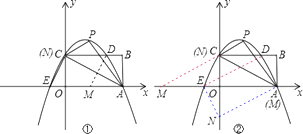
②若DE是平行四边形的边,
过点A作AN∥DE交y轴于N,四边形DANE是平行四边形,
∴DE=AN= ![]() =
= ![]() =2,
=2,
∵tan∠EAN= ![]() ,
,
∴∠EAN=30°,
∵∠DEA=∠EAN,
∴∠DEA=30°,
∴M( ![]() ,0),N(0,﹣1);
,0),N(0,﹣1);
同理过点C作CM∥DE交y轴于N,四边形CMDE是平行四边形,
∴M(﹣ ![]() ,0),N(0,1).
,0),N(0,1).
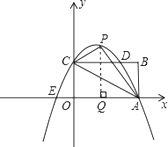
【解析】(1)根据OC、OA的长,可求得∠OCA=∠ACP=60°(折叠的性质),∠BCA=∠OAC=30°,由此可判断出∠PCB的度数.(2)过P作PQ⊥OA于Q,在Rt△PAQ中,易知PA=OA=3,而∠PAO=2∠PAC=60°,即可求出AQ、PQ的长,进而可得到点P的坐标,将P、A坐标代入抛物线的解析式中,即可得到b、c的值,从而确定抛物线的解析式,然后将C点坐标代入抛物线的解析式中进行验证即可.(3)根据抛物线的解析式易求得C、D、E点的坐标,然后分两种情况考虑:
①DE是平行四边形的对角线,由于CD∥x轴,且C在y轴上,若过D作直线CE的平行线,那么此直线与x轴的交点即为M点,而N点即为C点,D、E的坐标已经求得,结合平行四边形的性质即可得到点M的坐标,而C点坐标已知,即可得到N点的坐标;
②DE是平行四边形的边,由于A在x轴上,过A作DE的平行线,与y轴的交点即为N点,而M点即为A点;易求得∠DEA的度数,即可得到∠NAO的度数,已知OA的长,通过解直角三角形可求得ON的值,从而确定N点的坐标,而M点与A点重合,其坐标已知;
同理,由于C在y轴上,且CD∥x轴,过C作DE的平行线,也可找到符合条件的M、N点,解法同上.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
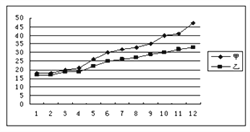
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员得分的平均数大于乙运动员得分的平均数
D. 甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张如图1的长为![]() ,宽为
,宽为![]() (
(![]() >
>![]() )的小长方形纸片,按图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则
)的小长方形纸片,按图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则![]() ,
,![]() 满足( )
满足( )

A.![]() =
=![]() B.
B.![]() =2
=2![]() C.
C.![]() =3
=3![]() D.
D.![]() =4
=4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和弟弟从家出发,步行去吉林省图书馆学习.出发2分钟后,小明发现弟弟的数学书忘记带了,弟弟继续按原速前往图书馆,小明按原路原速返回家取书,然后骑自行前往图书馆,恰好与弟弟同时到达图书馆.小明和弟弟各自距家的路程y(m)与小明步行的时间x(min)之间的函数图象如图所示.

(1)求a的值.
(2)求小明取回书后y与x的函数关系式.
(3)直接写出小明取回书后与弟弟相距100m的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车作为一种低碳、时尚、绿色的出行方式,它俨然成为市民出行的“新宠”.某公司准备安装A款共享单车,完成5760辆该款共享单车投入市场运营的计划.由于抽调不出足够的熟练工人完成安装,公司准备招聘一批新工人,将他们培训到能独立进行安装后上岗。生产开始后发现:4名熟练工人和5名新工人每天共安装88辆共享单车;2名熟练工人每天安装的共享单车数与3名新工人每天安装的共享单车数一样多.
(1)求每名熟练工人和新工人每天分别可以安装多少辆共享单车?
(2)若公司招聘m名新工人,使得招聘的新工人和抽调的熟练工人刚好一个月(30天)完成安装任务,已知工人们安装的共享单车中不能正常投入运营的占4%,且招聘的新工人数比抽调的熟练工人数少,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com