
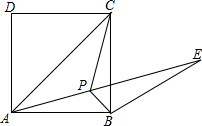
 如图,已知点P为正方形ABCD内一点,∠BAP=∠BCP=15°.
如图,已知点P为正方形ABCD内一点,∠BAP=∠BCP=15°.分析 (1)只要证明∠PAC=∠PCA即可.
(2)连接CE,在PE上截取一点N使得CN=CP,先证明△BCE,△CPN多少等边三角形,再证明△CBP≌△CEN即可解决问题.
(3)延长BP交AC于点O,在RT△POC中求出OC,即可解决问题.
解答 (1)证明:如图,∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°,∠BAC=∠BCA=45°,
∵∠BAP=∠BCP=15°,
∴∠PAC=∠PCA=30°,
∴PA=PC.
(2)结论:PE=PA+PB.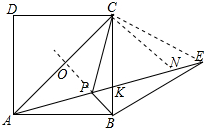
证明:连接CE,在PE上截取一点N使得CN=CP,
∵BE=BC=AB,
∴∠BAE=∠BEA=15°,
∴∠ABE=180°-∠BAE-∠BEA=150°,∵∠ABC=90°,
∴∠CBE=60°,∵BC=BE,
∴△BCE是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∵∠PCK+∠CPK+∠CKP=180°,∠BKE+∠KBE+∠BEK=180°,∠PKC=∠BKE,∠PCK=∠AEB=15°,
∴∠CPK=∠KBE=60°,∵CP=CN,
∴△CPN是等边三角形,
∴∠PCN=∠BCE=60°,CP=CN=PN,
∴∠PCB=∠ECN,
在△CBP和△CEN中,
$\left\{\begin{array}{l}{CB=CE}\\{∠PCB=∠ECN}\\{CP=CN}\end{array}\right.$,
∴△CBP≌△CEN,
∴PB=EN,∵PA=PC=PN,
∴PE=PN+NE=PC+PB=PA+PB.
(3)延长BP交AC于点O,
∵PA=PC,BA=BC,
∴PB垂直平分线段AC,
∴AO=OC,∠POC=90°,
∵∠PCO=30°,PC=2,
∴PO=$\frac{1}{2}$PC=1,OC=OA=$\sqrt{P{C}^{2}-P{O}^{2}}$=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
设AD=CD=a,则a2+a2=(2$\sqrt{3}$)2,
∵a>0,
∴a=$\sqrt{6}$,
∴AD=$\sqrt{6}$.
故答案为$\sqrt{6}$.
点评 本题考查全等三角形的判定和性质、正方形的性质、勾股定理等知识,解题的关键是添加辅助线构造全等三角形,出现60°要想到这种辅助线的添加方法,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 0.654×106 | B. | 6.54×106 | C. | 6.54×105 | D. | 65.4×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.696 3×106 | B. | 6.963×105 | C. | 69.63×104 | D. | 696.3×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a是负数 | |
| B. | 两个相似图形是位似图形 | |
| C. | 随机抛掷一枚质地均匀的硬币,落地后正面朝上 | |
| D. | 平移后的图形与原来对应线段相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
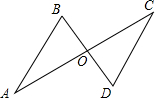 如图所示,△AOB≌△COD,A与C是对应点,那么下列结论中错误的是( )
如图所示,△AOB≌△COD,A与C是对应点,那么下列结论中错误的是( )| A. | ∠B=∠D | B. | ∠AOB=∠COD | C. | AC=BD | D. | AO=CO |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com