
分析 (1)先算平方,特殊角的三角函数值二次根式,再计算加减法即可求解;
(2)原式小括号中两项通分并利用同分母分式的减法法则计算,再将除法变为乘法,约分后根据同分母分式的加法法则计算得到最简结果,再把化简后x与y的值代入计算即可求出值.
解答 解:(1)sin223°-$\frac{1}{{2}^{2}}$+$\sqrt{27}$-$\sqrt{(si{n}^{2}30°-tan45°)^{2}}$+sin267°
=sin223°+cos223°-$\frac{1}{4}$+3$\sqrt{3}$-(1-$\frac{1}{4}$)
=1-$\frac{1}{4}$+3$\sqrt{3}$-1+$\frac{1}{4}$
=3$\sqrt{3}$;
(2)∵x=4cos30°-(-1)0=2$\sqrt{3}$-1,y=2tan60°=2$\sqrt{3}$,
∴(1-$\frac{2x}{x+y}$)÷$\frac{{x}^{2}-2xy+{y}^{2}}{3x+3y}$+$\frac{{x}^{2}+xy}{{x}^{2}-{y}^{2}}$
=$\frac{y-x}{x+y}$×$\frac{3(x+y)}{(x-y)^{2}}$+$\frac{x}{x-y}$
=-$\frac{3}{x-y}$+$\frac{x}{x-y}$
=$\frac{x-3}{x-y}$
=$\frac{2\sqrt{3}-1-3}{2\sqrt{3}-1-2\sqrt{3}}$
=4-2$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:解答题
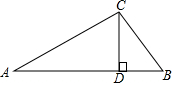 有一种屋顶的截面形状为三角形(如图),从屋子的最高处C点立一条垂直于横梁AB的支柱CD,已知AC=20,BC=15,DB=9,△ABC是直角三角形吗?说明理由.
有一种屋顶的截面形状为三角形(如图),从屋子的最高处C点立一条垂直于横梁AB的支柱CD,已知AC=20,BC=15,DB=9,△ABC是直角三角形吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
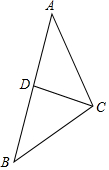 如图,已知在△ABC中,D为AB的中点,按要求完成下列各小题(保留作图痕迹,不要求写作法)
如图,已知在△ABC中,D为AB的中点,按要求完成下列各小题(保留作图痕迹,不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
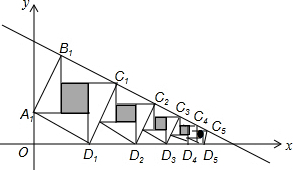 赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=-$\frac{1}{2}$x+$\frac{7}{2}$上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为$({\frac{2}{3})}^{2n-2}$.
赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=-$\frac{1}{2}$x+$\frac{7}{2}$上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为$({\frac{2}{3})}^{2n-2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com