
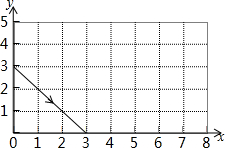
 如图,一点光源在(0,3)处,沿所示的方向发射,长方形四条边上有四个平面镜,与坐标平面垂直放置,设第一个入射点P1坐标为(3,0),则第二个入射点P2(6,3),第三个入射点P3(3,6),作出光路图,并写出第2013个入射点P2013(3,0)
如图,一点光源在(0,3)处,沿所示的方向发射,长方形四条边上有四个平面镜,与坐标平面垂直放置,设第一个入射点P1坐标为(3,0),则第二个入射点P2(6,3),第三个入射点P3(3,6),作出光路图,并写出第2013个入射点P2013(3,0)  备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2012 | D. | 2013 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
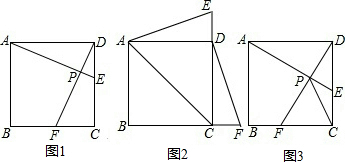
 如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.
如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
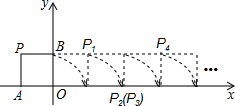 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2003次,点P依次落在点P1、P2、P3、P4…Pn的位置,则P2003的横坐标x2003=2002.
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2003次,点P依次落在点P1、P2、P3、P4…Pn的位置,则P2003的横坐标x2003=2002.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,求他一次就能猜中的概率.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,求他一次就能猜中的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com