【题目】如图，在ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．
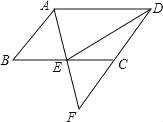
（1）求证：AB=CF；
（2）连接DE，若AD=2AB，求证：DE⊥AF．
【答案】（1）证明过程见解析；（2）证明过程见解析.
【解析】
试题分析：（1）由在ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AB∥DF， ∴∠ABE=∠FCE， ∵E为BC中点， ∴BE=CE，
在△ABE与△FCE中，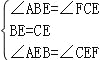
， ∴△ABE≌△FCE（ASA）， ∴AB=FC；
（2）∵AD=2AB，AB=FC=CD， ∴AD=DF， ∵△ABE≌△FCE， ∴AE=EF， ∴DE⊥AF．
科目：初中数学 来源： 题型：
【题目】平面直角坐标系中，下列各点中，在y轴上的点是 ( )
A. ( 2，0 ) B. ( -2，3 ) C. ( 0，3 ) D. ( 1，-3 )
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列语句中：①一条直线有且只有一条垂线；②不相等的两个角一定不是对顶角；③两条不相交的直线叫做平行线；④若两个角的一对边在同一直线上，另一对边互相平行，则这两个角相等；⑤不在同一直线上的四个点可画6条直线。其中错误的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作正方形ADEF，连接CF．
（1）如图1，当点D在线段BC上时，求证：①BD⊥CF．②CF=BC﹣CD．
（2）如图2，当点D在线段BC的延长线上时，其它条件不变，请直接写出CF、BC、CD三条线段之间的关系；
（3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系．②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
（1）求证：CD是⊙O的切线；
（2）过点B作⊙O的切线交CD的延长线于点E，BC=6， 
．求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】光年是天文学中的距离单位，1光年大约是9500 000 000 000km，这个数据用科学记数表示是（ ）
A. 0.95×1013km B. 950×1010km C. 95×1011km D. 9.5×1012km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com