
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
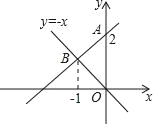
【答案】(1)一次函数的解析式为y=x+2;(2)1.
【解析】
(1)根据点B在函数y=﹣x上,点B的横坐标为﹣1,可以求得点B的坐标,再根据一次函数过点A和点B即可求得一次函数的解析式;
(2)将y=0代入(1)求得的一次函数的解析式,求得该函数与x轴的交点,即可求得一次函数图象、正比例函数图象与x轴围成的三角形的面积.
(1)设一次函数的解析式为:y=kx+b.
∵点B在函数y=﹣x上,点B的横坐标为﹣1,∴当x=﹣1时,y=﹣(﹣1)=1,∴点B的坐标为(﹣1,1).
∵点A(0,2),点B(﹣1,1)在一次函数y=kx+b的图象上,∴![]() ,得:
,得:![]() ,即一次函数的解析式为y=x+2;
,即一次函数的解析式为y=x+2;
(2)将y=0代入y=x+2,得:x=﹣2,则一次函数图象、正比例函数图象与x轴围成的三角形的面积为:![]() 1.
1.


科目:初中数学 来源: 题型:
【题目】我们知道,同底数幂的乘法法则为am·an=am+n(其中a≠0 ,m、n为正整数),类似地我们规定关于任意正整数m、n的一种新运算:h(m+n)=h(m)·h(n);比如h(2)=3,则h(4)=h(2+2)=3×3=9,若h(2)=k(k≠0 ),那么h(2n)·h(2020)的结果是( )
A.2k+2020B.2k+1010C.kn+1010D.1022k
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线OB平分∠AOC,∠AOC的余角比∠BOC小42°.
(1)求∠AOB的度数:
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数
(3)在(2)的条件下,画∠AOD的角平分线OE,则∠BOE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() , AD=4.
, AD=4.

(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )

A.①②③ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是
A. 红红不是胜就是输,所以红红胜的概率为![]()
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为![]()
D. 娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性;
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
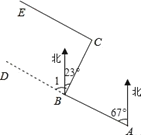
【题目】如图,某工程队从A点出发,沿北偏西67°方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23°的方向继续修建BC段,到达C点又改变方向,从C点继续修建CE段,∠ECB应为多少度,可使所修路段CE∥AB?试说明理由.此时CE与BC有怎样的位置关系?
以下是小刚不完整的解答,请帮他补充完整.
解:由已知平行,得∠1=∠A=67°(两直线平行, )
∴∠CBD=23°+67°= °,
当∠ECB+∠CBD= °时,
可得CE∥AB.( )
所以∠ECB= °
此时CE⊥BC.( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com