
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

【答案】(1)见解析;(2) 猜想:DM=AM. 理由见解析.
【解析】
(1)根据等边三角形的性质得出相等的角,相等的边,再等量代换即可得证;
(2)根据题意画出图形,根据轴对称的性质,得∠MDC=∠EDC,DE=DM,然后根据(1)的结论和等边三角形的性质证明即可.
(1)证明:∵△ABC是等边三角形,∴∠BAC=∠ACB=60°.
又∵∠BAD+∠DAC=∠BAC,∠EDC+∠DEC=∠ACB,
∴∠BAD+∠DAC=∠EDC+∠DEC.
∵DE=DA,∴∠DAC=∠DEC,
∴∠BAD=∠EDC.
(2)解:按题意画图如图所示.
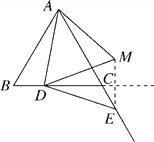
猜想:DM=AM.
理由如下:∵点M、E关于直线BC对称,
∴∠MDC=∠EDC,DE=DM.
又由(1)知∠BAD=∠EDC,∴∠MDC=∠BAD.
∵∠ADC=∠BAD+∠B,即∠ADM+∠MDC=∠BAD+∠B,
∴∠ADM=∠B=60°.
又∵DA=DE=DM,
∴△ADM是等边三角形,
∴DM=AM.


科目:初中数学 来源: 题型:
【题目】某校为表彰在“书香校园”活动中表现积极的同学,决定购买笔记本和钢笔作为奖品.已知5个笔记本、2支钢笔共需要100元;4个笔记本、7支钢笔共需要161元
(1)笔记本和钢笔的单价各多少元?
(2)恰好“五一”,商店举行“优惠促销”活动,具体办法如下:笔记本9折优惠;钢笔10支以上超出部分8折优惠若买x个笔记本需要y1元,买x支钢笔需要y2元;求y1、y2关于x的函数解析式;
(3)若购买同一种奖品,并且该奖品的数量超过10件,请你分析买哪种奖品省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() .善于思考的小明进行了以下探索:
.善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() ,
,![]() .这样小明就找到了一种把类似
.这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法解决下列问题:
(1)当![]() 、
、![]() 、
、![]() 、
、![]() 均为正整数时,若
均为正整数时,若![]() ,用含
,用含![]() 、
、![]() 的式子分别表示
的式子分别表示![]() 、
、![]() ,得
,得![]() _________,
_________,![]() _________.
_________.
(2)利用所探索的结论,填空:![]() (_____+_____
(_____+_____![]() )2;
)2;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均为正整数,求
均为正整数,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:要将一块直径为![]() 的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.
的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.

操作:
方案一:在图![]() 中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
方案二:在图![]() 中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图).
中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图).
探究:
![]() 求方案一中圆锥底面的半径;
求方案一中圆锥底面的半径;
![]() 求方案二中半圆圆心为
求方案二中半圆圆心为![]() ,圆柱两个底面圆心为
,圆柱两个底面圆心为![]() 、
、![]() ,圆锥底面的圆心为
,圆锥底面的圆心为![]() ,试判断以
,试判断以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是什么样的特殊四边形,并加以证明.
为顶点的四边形是什么样的特殊四边形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x–2)(x–3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是
A. 当m=0时,x1=2,x2=3
B. m>–![]()
C. 当m>0时,2<x1<x2<3
D. 二次函数y=(x–x1)(x–x2)+m的图象与x轴交点的坐标为(2,0)和(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=BC,∠ACB=90°,CE与AB相交于点D,且BE⊥CE,AF⊥CE,垂足分别为点E、F.
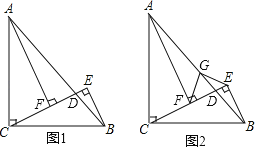
(1)若AF=5,BE=2,求EF的长.
(2)如图2,取AB中点G,连接FC、EC,请判断△GEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com