
 在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程
在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程 的两个根,且OA>OB.
的两个根,且OA>OB.
 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?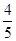 (2)
(2)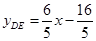 ,yDE=
,yDE= 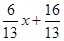 △AOE∽△DAO(3)F1 (3 , 8) ; F2 (-3 , 0) ; F3 (
△AOE∽△DAO(3)F1 (3 , 8) ; F2 (-3 , 0) ; F3 (
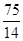 ,
,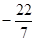 ); F4(-
); F4(-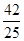 ,
,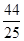 )
)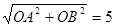
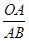 =
=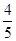 ······················· 1分
······················· 1分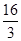 有
有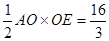
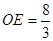 ∴E(
∴E(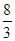 ,0)或E(—
,0)或E(—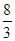 ,0)················· 1分
,0)················· 1分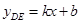 ,
, 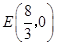 时有
时有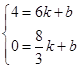
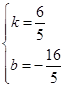
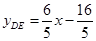 ···························· 1分
···························· 1分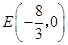 时,yDE=
时,yDE= 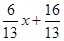 ·················· 1分
·················· 1分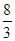
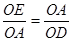

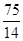 ,
,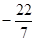 ); F4(-
); F4(-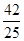 ,
,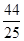 )
)

科目:初中数学 来源:不详 题型:解答题
 地出发向
地出发向 地行走,同时晓阳从
地行走,同时晓阳从 地出发向
地出发向 地行走,如图所示,相交于点M的两条线段
地行走,如图所示,相交于点M的两条线段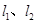 分别表示小明、晓阳离A地的距离
分别表示小明、晓阳离A地的距离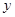 (千米)与已用时间
(千米)与已用时间 (分钟)之间的关系,
(分钟)之间的关系,
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 )本。
)本。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com