
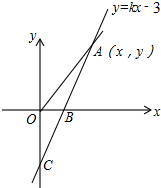
 如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB
如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB分析 (1)先确定出OC,进而得出OB,即可得出点B坐标,将点B的坐标代入直线解析式中即可得出k;
(2)直接利用三角形的面积公式即可得出结论;
(3)设出点P的坐标,进而利用两点间的距离公式求出OA2,OP2,AP2,分三种情况用两边相等建立方程求解即可.
解答 解:(1)在y=kx-3中,当x=0,得y=-3
∴OC=3,
∵OC=2OB,
∴OB=1.5
∴B(1.5,0)
把x=1.5,y=0代入y=kx-3中
∴k=2,
(2)由(1)知OB=1.5,点A在直线y=2x-3上,
S=$\frac{1}{2}$OB•|yA|
=$\frac{1}{2}$×1.5×(2x-3)
=$\frac{3}{2}$x-$\frac{9}{4}$(x>0)
(3)①由(2)知S=$\frac{3}{2}$x-$\frac{9}{4}$,
∵△ABO的面积为$\frac{9}{4}$,
$\frac{3}{2}$x-$\frac{9}{4}$=$\frac{9}{4}$
∴x=3,
∴y=2x-3=3,
∴A(3,3)
当A运动到(3,3)时△AOB面积为$\frac{9}{4}$;
②由(1)知,A(3,3),
设点P(m,0),
∴OA2=18,OP2=m2,AP2=(m-3)2+9
∵△AOP为等腰三角形,(如图)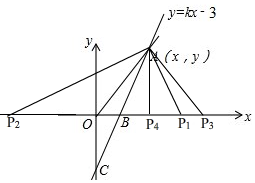
∴Ⅰ、当OA=OP时,OA2=OP2,
即:18=m2,
∴m=±3$\sqrt{2}$,
∴P1(3$\sqrt{2}$,0),P2(-3$\sqrt{2}$,0)
Ⅱ、当OA=AP时,OA2=AP2,
即:18=(m-3)2+9,
∴m=0(此时和点A重合,所以舍去)或m=6,
∴P3(6,0)
Ⅲ、当OP=AP时,OP2=AP2,
即:m2=(m-3)2+9,
∴m=3,
∴P4(3,0)
即:满足条件的点P的坐标为(-3$\sqrt{2}$,0)、(3,0)、(3$\sqrt{2}$,0)、(6,0).
点评 此题是一次函数综合题,主要考查了待定系数法,三角形的面积公式,等腰三角形的性质,解(1)的关键是求出OC,解(3)的关键是用方程的思想解决问题,是一道基础题目.


科目:初中数学 来源: 题型:选择题
 如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )
如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )| A. | 5+$\sqrt{2}$+$\sqrt{7}$ | B. | 5+$\sqrt{2}$+$\sqrt{13}$ | C. | $\sqrt{2}$+$\sqrt{13}$+$\sqrt{17}$ | D. | $\sqrt{2}$+$\sqrt{58}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
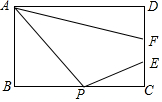 如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | m |
| B | 地面灰尘大,空气湿度低 | 20 |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 80 |
| E | 其他 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com