
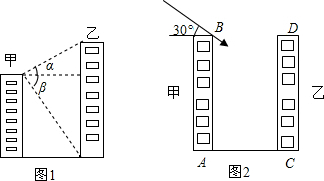
分析 (1)在Rt△ABD和Rt△ABC中,分别表示出BD、BC,继而可得CD的长度;
(2)在Rt△BDE中表示出DE,继而求出CE.
解答 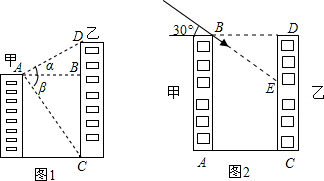 解:(1)如图1所示:
解:(1)如图1所示:
在Rt△ABD中,BD=ABtan∠BAD=40tanα,
在Rt△ABC中,BC=ABtan∠BAC=ABtanβ,
则可得CD=AB(tanα+tanβ).
(2)如图2所示:
在Rt△BDE中,DE=BDtan∠DBE=BDtan30°=8$\sqrt{3}$m,
则CE=CD-DE=(30-8$\sqrt{3}$)m.
答:甲楼的影子在乙楼上有(30-8$\sqrt{3}$)m高.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解,难度一般.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
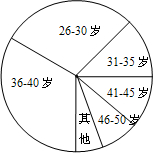 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:| 关心问题 | 频数 | 频率 |
| 收入分配 | 90 | 0.25 |
| 住房问题 | 54 | 0.15 |
| 物价调控 | 36 | 0.1 |
| 医疗改革 | 18 | 0.05 |
| 养老保险 | 54 | 0.15 |
| 其他 | 108 | 0.30 |
| 合计 | 360 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
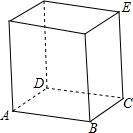 如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.
如图是一个长方体,AB=x,BC=$\frac{6}{5}$x,CE=10,则长方体的体积y与x之间的函数解析式是y=12x2,y是x的二次函数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
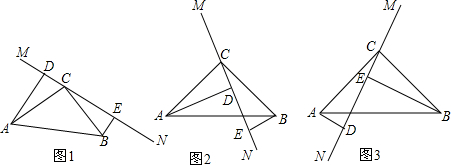
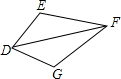 填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.
填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.
如图:O是矩形ABCD对角线AC、BD的交点,过点D作DE∥AC,过点C作CE∥BD,DE、CE相交于点E,连结OE交CD于点F,那么OE与DC垂直吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
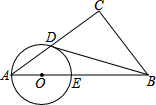 已知Rt△ABC中,∠C=90°,点O在AB上,以O为圆心OA为半径的圆与AC、AB分别交于点D、E,且∠A=∠CBD.
已知Rt△ABC中,∠C=90°,点O在AB上,以O为圆心OA为半径的圆与AC、AB分别交于点D、E,且∠A=∠CBD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
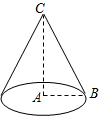 如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )| A. | 9π | B. | 12π | C. | 15π | D. | 20π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com