Question

（1）火车长为400米，通过隧道（从火车头进入隧道至车尾离开隧道）需10分钟，若每分钟速度增加0.1千米，则只需9分钟．求隧道长．
（2）甲、乙两人两次到某粮店去买大米，两次的大米价格分别为每斤a元和b元（a≠b），甲每次买100斤大米，乙每次买100元的大米，问谁两次买的大米平均价格更低些？说明理由．

Answer 1

解：（1）设隧道长为x米．
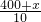
+100=，
解得x=8600．
答：隧道长8600米．
（2）甲的平均价格为：=；
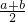
乙的平均价格为：=；
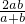
∵（a-b）²＞0（a≠b），
∴a²+b²＞2ab，
∴（a+b）²＞4ab，
两边都除以2（a+b）得，
＞，
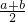
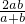
答：乙买的价格低一些．
分析：（1）关系式为：（火车长+隧道长）÷10+100=（火车长+隧道长）÷9，把相关数值代入求值即可；
（2）平均价格=总价÷总数量，把相关数值代入后，比较即可．
点评：考查一元一次方程的应用及分式的比较；得到速度的等量关系及使用（a-b）²＞0（a≠b），是解决这两个问题的关键．