
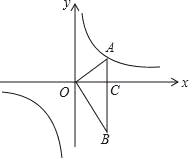
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上是否存在一点P,使得S△AOP=![]() S△AOB,若存在,求所有符合条件点P的坐标;若不存在,简述你的理由.
S△AOB,若存在,求所有符合条件点P的坐标;若不存在,简述你的理由.
【答案】(1)y=![]() ;(2)(﹣2
;(2)(﹣2![]() ,0)或(2
,0)或(2![]() ,0)
,0)
【解析】
(1)把A的坐标代入反比例函数的表达式,即可求出答案;
(2)求出∠A=60°,∠B=30°,求出线段OA和OB,求出△AOB的面积,根据已知S△AOP![]() S△AOB,求出OP长,即可求出答案.
S△AOB,求出OP长,即可求出答案.
(1)把A(![]() ,1)代入反比例函数y
,1)代入反比例函数y![]() 得:k=1
得:k=1![]() ,所以反比例函数的表达式为y
,所以反比例函数的表达式为y![]() ;
;
(2)∵A(![]() ,1),OA⊥AB,AB⊥x轴于C,∴OC
,1),OA⊥AB,AB⊥x轴于C,∴OC![]() ,AC=1,OA
,AC=1,OA![]() 2.
2.
∵tanA![]() ,∴∠A=60°.
,∴∠A=60°.
∵OA⊥OB,∴∠AOB=90°,∴∠B=30°,∴OB=2OC=2![]() ,∴S△AOB
,∴S△AOB![]() OAOB
OAOB![]() 2×2
2×2![]() .
.
∵S△AOP![]() S△AOB,∴
S△AOB,∴![]() OP×AC
OP×AC![]() .
.
∵AC=1,∴OP=2![]() ,∴点P的坐标为(﹣2
,∴点P的坐标为(﹣2![]() ,0)或(2
,0)或(2![]() ,0).
,0).


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
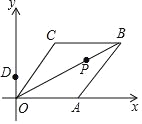
【题目】如图,已知菱形OABC的边OA在x轴上,点B的坐标为(8,4),P是对角线OB上的一个动点,点D(0,1)在y轴上,当PC+PD最短时,最短距离是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
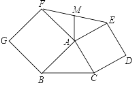
【题目】已知:如图,在△ABC中,cos∠ABC=![]() ,sin∠ACB=
,sin∠ACB=![]() ,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为_____.
,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋装有编号为1,2,3的三个形状、大小、材质等相同的小球,从袋中随意摸出1个球,记事件A为“摸出的球编号为奇数”,随意抛掷一个之地均匀正方体骰子,六个面上分别写有1﹣6这6个整数,记事件B为“向上一面的数字是3的整数倍”,请你判断等式“P(A)=2P(B)”是否成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
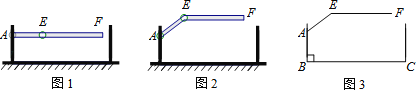
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向, B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
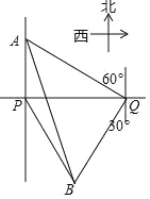
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调研发现:某品牌童装平均每天可售出 20 件,每件盈利 40元.在每件降价幅度不超过 18 元的情况下,若每件童装降价 1 元,则每天可多售出 2 件,设降价 x 元.
(1)降价 x 元后,每件童装盈利是多少元,每天销售量是多少件;
(2)要想每天销售这种童装盈利 1200 元,那么每件童装应降价多少元?
(3)每天能盈利 1800 元吗?如果能,每件童装应降价多少元?如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com