练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．在△ABC中，AD是角平分线，AB=24，AC=36，S△ABD=S△ADC，此题中“角平分线”这个条件的作用是角的平分线上的点到角的两边的距离相等．

    分析 根据角的平分线上的点到角的两边的距离相等解答即可．

    解答 解：因为角平分线到角两边的距离相等，即DE=DF，
    所以S△ABD=S△ADC，
    利用的是角的平分线上的点到角的两边的距离相等；
    故答案为：S△ADC；角的平分线上的点到角的两边的距离相等．

    点评 本题考查了角平分线的性质；要熟练掌握角平分线的性质，会求三角形的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．下列变形中不正确的是（　　）
    A．若5x+8=4x，则5x-4x=8B．若3x-1=x+3，则2x=4
    C．若2=x，则x=2D．若x-1=3，则x=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，直线AB，CD相交于点O，∠EOD=90°，若∠AOE=2∠AOC，则∠DOB的度数为（　　）
    A．25°B．30°C．45°D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

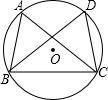    9．如图，点A，B，C，D是⊙O上的四点，且$\widehat{AB}$=$\widehat{CD}$，AC=DB．
    （1）求证：△ABC≌△DCB；
    （2）若∠A=60°，BC=1，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，已知线段AB=4cm．
    （1）读句画图：延长线段AB到点C，使得AB=2BC．
    （2）在（1）的条件下，若点P是线段AC的中点，求线段PB的长．
    （3）延长线段AB到点C，若点P是线段AC的中点，点Q是BC的中点，求线段PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．已知a+$\frac{1}{a}$=$\sqrt{10}$，则a-$\frac{1}{a}$的值为（　　）
    A．2B．6C．±$\sqrt{6}$D．±2$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列式子（1）$\sqrt{6}$，（2）$\sqrt{{a}^{2}+1}$，（3）$\root{3}{9}$，（4）$\sqrt{{a}^{2}+2a+1}$，（5）$\sqrt{|{m}^{2}-1|}$中，是二次根式的是（　　）
    A．（1）（2）（3）（4）B．（2）（3）（4）（5）C．（1）（2）（3）（5）D．（1）（2）（4）（5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．某中学举行“校园•朗读者”朗诵大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
    （1）根据图示填写表格；
    （2）结合两队成绩的平均数和中位数，初中队的决赛成绩较好；
    （3）已知高中代表队决赛成绩的方差为160，计算初中代表队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．（方差公式：S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]
    平均分（分）中位数（分）众数（分）
    初中部858585
    高中部8580100

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，已知∠APN=30°，则轮船A在灯塔P的北偏东30°的方向上；轮船B在灯塔P的南偏东70°的方向上，则∠APB=80度，若轮船C在∠APB的角平分线上，则轮船C在灯塔P的北偏东70°的方向上．

    查看答案和解析>>

    同步练习册答案