
如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为 米.
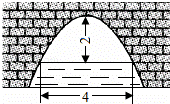
 解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,

抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,其中a可通过代入A点坐标(﹣2,0),
到抛物线解析式得出:a=﹣0.5,所以抛物线解析式为y=﹣0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,
可以通过把y=﹣1代入抛物线解析式得出:
﹣1=﹣0.5x2+2,
解得:x=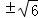 ,
,
所以水面宽度增加到 米,
米,


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
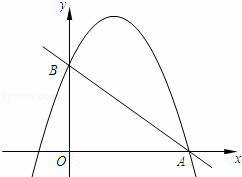
如图,在平面直角坐标系xOy中,点A坐标为(8,0),点B在y轴的正半轴上,且cot∠OAB= ,抛物线y=﹣
,抛物线y=﹣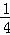 x2+bx+c经过A、B两点.
x2+bx+c经过A、B两点.
(1)求b、c的值;
(2)过点B作CB⊥OB,交这个抛物线于点C,以点C为圆心,CB为半径长的圆记作圆C,以点A为圆心,r为半径长的圆记作圆A.若圆C与圆A外切,求r的值;
(3)若点D在这个抛物线上,△AOB的面积是△OBD面积的8倍,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ,
, ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
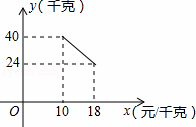
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com