
����Ŀ���ҹ��Ŵ���ѧ������ֶ���λ������ǰ�У����С�������ǡ�����һ������ͼ����������εĹ��취�������ϵ�������1������ÿ������Ϊ���Ϸ���������֮�ͣ��������ˣ�a+b��n��nΪ����������չ��ʽ����a�Ĵ����ɴ�С��˳�����У���ϵ�����ɣ����磬���������е����е�������1��2��1��ǡ�ö�Ӧ��a+b��2=a2+2ab+b2չ��ʽ�е�ϵ���������е��ĸ���1��3��3��1��ǡ�ö�Ӧ�ţ�a+b��3=a3+3a2b+3ab2+b2չ��ʽ�е�ϵ���ȵȣ� 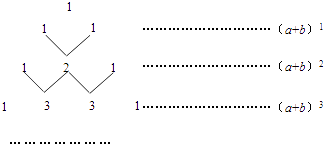
��1����������Ĺ��ɣ���a+b��5��չ��ʽ= ��
��2����������Ĺ��ɼ��㣺25��5��24+10��23��10��22+5��2��1= ��
���𰸡�
��1����a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
��2��1
���������⣺��1.���ߣ�a+b��1=a+b�� ��a+b��2=a2+2ab+b2 ��
��a+b��3=a3+3a2b+3ab2+b3 ��
��a+b��4=a4+4a3b+6a2b2+4ab3+b4 ��
�ࣨa+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 ��
���Դ��ǣ���a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5��
��2.��25��5��24+10��23��10��22+5��2��1=��2��1��5=15=1�����ݣ�a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5�������õó��ģ������Դ��ǣ�1��
�����㾫�����������⣬������Ҫ�˽���ȫƽ����ʽ(��ƽ����ĩƽ����������ĩ�����룮�͵�ƽ�����ټӣ��ȼ���Ӳ�ƽ��)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����E��F�ֱ���ֱ��AB��CD�ϣ���P��AB��CD֮�䣬����EP��FP����ͼ1����FP�ϵĵ�G��GH��EP����CD�ڵ�H���ҡ�1=��2��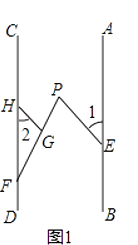
��1����֤��AB��CD��
��2����ͼ2��������FC��FP�۵�����PE�ڵ�J����JKƽ�֡�EJF����JK��AB�����BEP���EPF֮���к�������ϵ����֤����Ľ��ۣ�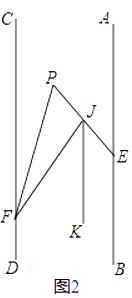
��3����ͼ3��������FC��FP�۵���������EA��EP�۵����۵���������߽��ڵ�M����EM��FMʱ�����EPF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ൺ�����������ߡ�������ɽ�ͼ�ī�ĵ���11����ȫ��Լ58km������58km�ÿ�ѧ�������ɱ�ʾΪ��������m��
A. 0.58��105B. 58��104C. 5.8��104D. 5.8��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������������������
A. ͬ���ڽǻ��� B. �����ε�һ����ǵ������������ڽ�֮��
C. ֱ������������ǻ��� D. �����ε�һ����Ǵ����ڽ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧȥ��ͨ������Ʒ���ա���O�ʽ���������ƶ��ɽ���С�Сѧ����27������������һ����ѧ����ѧϰ������ҪxԪ������һ��Сѧ����ѧϰ������ҪyԪ�����꼶ѧ���O�ʽ���������ǡ�������С�Сѧ�������IJ���������±���
�꼶 | �O�ʽ����� | ����ƶ����ѧ | ����ƶ��Сѧ������������ |
���꼶 | 5000 | 2 | 5 |
���꼶 | 6000 | 3 | 5 |
���꼶 | 8000 |
��1����x��y��ֵ��
��2�����꼶ѧ���O���ʽ������������ƶ���С�Сѧ����ѧϰ���ã�������꼶ѧ��������ƶ���С�Сѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڼ䣬ijѧУ�ƻ��ò�ɫ�ĵ���ש�����ѧ¥��ǰһ����βٳ�ABCD�ĵ��森��֪������βٳ�����ij�Ϊ100m����Ϊ80m��ͼ�������ͼ��ʾ���ٳ����Ľ�ΪС�����Σ���Ӱ����Ϊ�ĸ����Σ��ĸ����εĿ���ΪС�����εı߳�����ʵ������Ĺ����ܣ���Ӱ�����̺�ɫ����ש�����ಿ���̻�ɫ����ש��
��1������ٳ����̻�ɫ����ש��������̺�ɫ����ש�����4������ô�ٳ��Ľǵ�ÿ��С�����α߳��Ƕ����ף�
��2�������ɫ����ש�ļ۸�Ϊÿƽ����30Ԫ����ɫ����ש�ļ۸�Ϊÿƽ����20Ԫ��ѧУ����15��Ԫ�ʽ�����Щ�ʽ��Ƿ��ܹ��������ȫ������ש������ܹ�����ѧ��ȫ������ש����ʣ���ʽ��Ƕ���Ԫ��������ܹ��������ȫ������ש�������ֻ�Ӧ�����ٸ�ѧУ��������ʽ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. 3a3+a3��4a6B. ��a+b��2��a2+b2
C. 5a��3a��2aD. ����a��2a3����a6
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com