
【题目】如图,△ABC中,∠ACB=90°, CD⊥AB于点D,∠A=30°,BD=1.5cm ,则AB=______cm.

【答案】6
【解析】在直角三角形ABC中,由∠A的度数求出∠B的度数,在直角三角形BCD中,可得出∠BCD度数为30°,根据直角三角形中,30°所对的直角边等于斜边的一半,得到BC=2BD,由BD的长求出BC的长,在直角三角形ABC中,同理得到AB=2BC,由BC的长即可求出AB的长.
解:∵△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°,又CD⊥AB,
∴∠BCD=30°,
在Rt△BCD中,∠BCD=30°,BD=1.5cm,
可得BC=2BD=3cm,
在Rt△ABC中,∠A=30°,BC=3cm,
则AB=2BC=6cm.
故答案为:6.
“点睛”此题考查了含30°角直角三角形的性质,以及三角形的内角和定理,熟练掌握性质是解本题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】说明命题“若a2>b2,则a>b.”是假命题,举反例正确的是( )
A. a=2,b=3B. a=﹣2,b=3C. a=3,b=﹣2D. a=﹣3,b=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式正确的是( )
A. (a+b)2=a2+b2 B. (x+6)(x﹣6)=x2﹣6
C. (2x+3)2=2x2﹣12x+9 D. (2x﹣1)2=4x2﹣4x+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+C的图象过点A(﹣3,0),C(0,3).
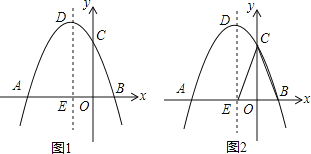
(1)求抛物线的解析式;
(2)探究:在抛物线的对称轴DE上是否存在点P,使得点P到直线AD和到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)探究:在对称轴DE左侧的抛物线上是否存在点F,使得2S△FBC=3S△EBC?若存在,求出点F的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 有两个角是直角的四边形是矩形;
B. 两条对角线相等的四边形是矩形;
C. 两条对角线垂直且相等的四边形是矩形;
D. 四个角都是直角的四边形是矩形;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com