
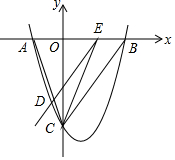
 如图,函数y=$\frac{1}{2}$x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,连接BC、AC.若AB和OC的长均为9,且AO<BO.
如图,函数y=$\frac{1}{2}$x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,连接BC、AC.若AB和OC的长均为9,且AO<BO.分析 (1)先根据OC的长求出c=9,再由根与系数的关系求出b=$±\frac{3}{2}$,由AO<OB得:抛物线的对称轴是y轴的右侧,即a、b异号,得出b的值;
(2)根据平行得相似:△ADE∽△ACB,所以面积比等于相似比的平方,则有$\frac{S}{{S}_{△ACB}}$=$\frac{A{E}^{2}}{A{B}^{2}}$,代入计算可以求出S关于m的函数关系式;
(3)根据等式S△CDE=S△ACE-S△ADE求出关系式,利用二次函数求最值,以点E为圆心,与BC相切的圆的半径是:过E与BC垂直的线段EF的长,根据相似求出EF的长,代入圆的面积公式求出面积即可.
解答 解:(1)∵OC=9,
∴C(0,-9),
∴c=-9,
设A(x1,0),B(x2,0),
∵AB=9,
∴x2-x1=9,
∴(x2-x1)2=81,
∵x1+x2=-2b,x1•x2=2c=-18,
∴${{x}_{1}}^{2}+{{x}_{2}}^{2}$-2x1x2=81,
(x1+x2)2-4x1x2=81,
(-2b)2-4×(-18)=81,
b=±$\frac{3}{2}$,
∵AO<BO,
∴抛物线的对称轴是y轴的右侧,
即a、b异号,
∵a=$\frac{1}{2}$>0,
∴b=-$\frac{3}{2}$;
(2)S△ACB=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×9×9=$\frac{81}{2}$,
∵ED∥BC,
∴△ADE∽△ACB,
∴$\frac{S}{{S}_{△ACB}}$=$\frac{A{E}^{2}}{A{B}^{2}}$,
∴$\frac{S}{\frac{81}{2}}$=$\frac{{m}^{2}}{{9}^{2}}$,
∴S=$\frac{1}{2}$m2,其中0<m<9;
(3)如图,S△CDE=S△ACE-S△ADE=$\frac{1}{2}$×m×9-$\frac{1}{2}{m}^{2}$,
S△CDE=-$\frac{1}{2}$(m-$\frac{9}{2}$)2+$\frac{81}{8}$,
∵-$\frac{1}{2}$<0,
∴当m=$\frac{9}{2}$时,S有最大值,且最大值为$\frac{81}{8}$,
y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9,
当y=0时,$\frac{1}{2}$x2-$\frac{3}{2}$x-9=0,
解得:x=6或-3,
∴A(-3,0),
∴OA=3,
∴OE=$\frac{9}{2}$-3=$\frac{3}{2}$,
∴E($\frac{3}{2}$,0),
∴BE=AB-AE=9-$\frac{9}{2}$=$\frac{9}{2}$,
BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{9}^{2}+{6}^{2}}$=3$\sqrt{13}$,
作EF⊥BC,垂足为F,
∵∠EBF=∠CBO,∠EFB=∠COB,
∴△EFB∽△COB,
∴$\frac{EF}{OC}=\frac{BE}{CB}$,
即$\frac{EF}{9}=\frac{\frac{9}{2}}{3\sqrt{13}}$,
∴EF=$\frac{27}{26}$$\sqrt{13}$,
∴⊙E的面积=π•EF2=π•($\frac{27}{26}$$\sqrt{13}$)2=$\frac{729}{52}$π,
答:以点E为圆心,与BC相切的圆的面积为$\frac{729}{52}π$.
点评 本题是二次函数的综合题,考查了利用根与系数的关系求二次函数的字母系数,明确若抛物线与x轴的两交点A(x1,0),B(x2,0),则x1+x2=-$\frac{b}{2a}$,x1•x2=$\frac{c}{a}$;把函数与几何图形联系起来,在求某三角形的最值问题时,将其转化为函数问题,利用配方法或顶点坐标求最值.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )
如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )| A. | -$\frac{5}{2}$ | B. | -$\frac{10}{3}$ | C. | -4 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
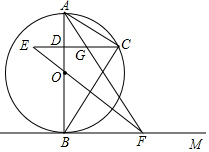 如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中始终保持OF∥AC.
如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中始终保持OF∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
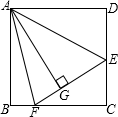 如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:
如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com