
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
科目:初中数学 来源: 题型:
【题目】骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“*”所代表的数是( )
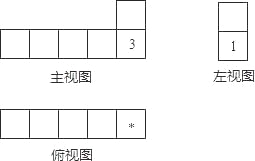
A. 2 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( ) 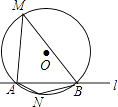
A.2 ![]()
B.4
C.4 ![]()
D.8 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿 ![]() 回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( ).
回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是( ).
A.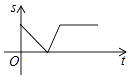
B.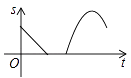
C.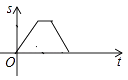
D.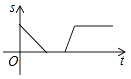
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 是否平行?为什么?
是否平行?为什么?
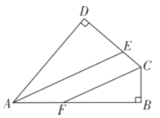
对于上述问题,小红给出了解答过程,请你在以下解答过程的括号内填上适当的内容
解:![]()
理由如下:
![]() ,
,
![]() .
.
∵四边形![]() 的内角和为360°,
的内角和为360°,
∴( ① )+( ② )=180°,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
![]() .
.
![]() .
.
又![]() , ( ③ )
, ( ③ )
![]() ,
,
![]() . ( ④ )
. ( ④ )
![]() .( ⑤ )
.( ⑤ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.
(1)求梯子顶端A离地面的高度AD的长和两梯脚之间的距离BC的长.
(2)生活经验告诉我们,增大两梯脚之间的距离可降低梯子的高度,若BC长达到6米,则梯子的高度下降多少米?(以上结果均精确到0.1米,供参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型的名称是
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足 ![]() a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=﹣m(m> ![]() )于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD;
(2)设△ACD的面积为S,求S关于m的函数关系式;
(3)若四边形ABCD恰有一组对边平行,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com