
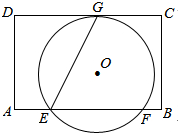
 如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=$\frac{1}{4}$AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=$\sqrt{5}$:2.当⊙O与边BC所在的直线与相切时,AB的长是12.
如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=$\frac{1}{4}$AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=$\sqrt{5}$:2.当⊙O与边BC所在的直线与相切时,AB的长是12. 分析 过点G作GN⊥AB,垂足为N,可得EN=NF,由EG:EF=$\sqrt{5}$:2,得:EG:EN=$\sqrt{5}$:1,依据勾股定理即可求得AB的长度.
解答  解:边BC所在的直线与⊙O相切时,
解:边BC所在的直线与⊙O相切时,
如图,过点G作GN⊥AB,垂足为N,
∴EN=NF,
又∵EG:EF=$\sqrt{5}$:2,
∴EG:EN=$\sqrt{5}$:1,
又∵GN=AD=8,
∴设EN=x,则GE=$\sqrt{5}$x,根据勾股定理得:
($\sqrt{5}$x)2-x2=64,解得:x=4,GE=4$\sqrt{5}$,
设⊙O的半径为r,由OE2=EN2+ON2
得:r2=16+(8-r)2,
∴r=5.∴OK=NB=5,
∴EB=9,
又AE=$\frac{1}{4}$AB,
∴AB=12.
故答案为:12.
点评 本题考查了切线的性质以及勾股定理和垂径定理的综合应用,解答本题的关键在于做好辅助线,利用勾股定理求出对应圆的半径.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7).
如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠C=90°,BC=4,AC=4$\sqrt{3}$,点D从A出发沿AB以每秒2个单位的速度向点B匀速运功,同时,点E从B出发沿BC以每秒1个长单位的速度向点C匀速运动,当一个点到达终点时,另一个点也停止运动,设点D、E运动的时间为t(t>0)作DF⊥AC于点F,连DE、EF.
如图,△ABC中,∠C=90°,BC=4,AC=4$\sqrt{3}$,点D从A出发沿AB以每秒2个单位的速度向点B匀速运功,同时,点E从B出发沿BC以每秒1个长单位的速度向点C匀速运动,当一个点到达终点时,另一个点也停止运动,设点D、E运动的时间为t(t>0)作DF⊥AC于点F,连DE、EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com