
【题目】如图,抛物线:y=ax2+bx+4与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行.当点M原点时,点Q立刻掉头并以每秒![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.

【答案】(1)抛物线的解析式是y=![]() x2+x+4;
x2+x+4;
(2)点T的坐标是(1,1);
(3)点M的运动时间t与△APQ面积S的函数关系式是S=t2+6t(0<t2),S=![]() t2+4t+3(2<t3),S的最大值是
t2+4t+3(2<t3),S的最大值是![]() .
.
【解析】试题分析:(1)把A、B的坐标代入抛物线的解析式得到方程组,求出方程组的解即可;(2)设直线x=1上一点T(1,h),连接TC、TA,作CE⊥直线x=1,垂足是E,根据TA=TC由勾股定理求出即可;(3)(I)当0<t≤2时,△AMP∽△AOC,推出比例式,求出PM,AQ,根据三角形的面积公式求出即可;(II)当2<t≤3时,作PM⊥x轴于M,PF⊥y轴于点F,表示出三角形APQ的面积,利用配方法求出最值即可.
试题解析:(1)把A(2,0),B(4,0)代入y=ax2+bx+4得:
![]() ,
,
解得:a=![]() ,b=1,
,b=1,
∴抛物线的解析式是:y=![]() x2+x+4,
x2+x+4,
答:抛物线的解析式是y=![]() x2+x+4.
x2+x+4.
(2)由y=![]() x2+x+4=
x2+x+4=![]() (x1)2+
(x1)2+![]() ,得抛物线的对称轴为直线x=1,
,得抛物线的对称轴为直线x=1,
直线x=1交x轴于点D,直线x=1上一点T(1,h),
连接TC、TA,作CE⊥直线x=1,垂足是E,
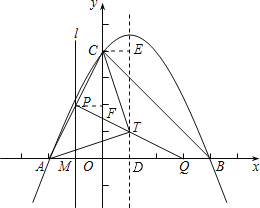
由C(0,4)得点E(1,4),
在Rt△ADT和Rt△TEC中,由TA=TC得32+h2=12+(4h)2,
∴h=1,
∴T的坐标是(1,1),
答:点T的坐标是(1,1).
(3)(I)当0<t2时,△AMP∽△AOC,
∴![]() ,PM=2t,
,PM=2t,
AQ=6t,
∴S=![]() PMAQ=
PMAQ=![]() ×2t(6t)=t2+6t=(t3)2+9,
×2t(6t)=t2+6t=(t3)2+9,
当t=2时S的最大值为8;
作PM⊥x轴于M,作PF⊥y轴于点F,
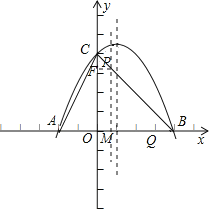
则△COB∽△CFP,
又∵CO=OB,
∴FP=FC=t2,PM=4(t2)=6t,AQ=4+32(t2)=32t+1,
∴S=![]() PMAQ=
PMAQ=![]() (6t)(
(6t)( ![]() t+1)=
t+1)= ![]() t2+4t+3=
t2+4t+3=![]() (t
(t![]() )2+
)2+![]() ,
,
当t=![]() 时,S最大值为
时,S最大值为![]() ,
,
综合(I)(II)S的最大值为![]() ,
,
答:点M的运动时间t与△APQ面积S的函数关系式是S=t2+6t(0<t2),S=![]() t2+4t+3(2<t3),S的最大值是
t2+4t+3(2<t3),S的最大值是![]() .
.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】下列多项式相乘,可以用平方差公式直接计算的是( )
A. (x+5y)(x-5y)B. (-x+y)(y-x)
C. (x+3y)(2x-3y)D. (3x-2y)(2y-3x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年盐城市中考考生约55800人,则数据55800用科学记数法可表示为( )
A.0.558×105
B.5.58×105
C.5.58×104
D.55.8×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形中ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN, AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系_____________________,并证明;
(2)位置关系_____________________,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
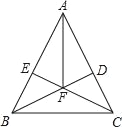
【题目】如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.
【答案】证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
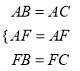 ,
,
∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.
【题型】解答题
【结束】
23
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
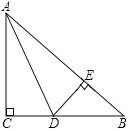
(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com