

分析 (1)利用等腰直角三角形的性质,全等三角形的判定,证明△BCE≌△ACD,然后利用全等三角形的性质,直角三角形的性质,等量代换,即可得出BE=2CF,利用三角形外角定理,等腰三角形性质∠EGF=∠BCF+∠CBE=∠BCF+∠ACF=∠ACB=90°,即可得到BE⊥CF;
(2)作辅助线,构建全等三角形,利用旋转的性质,找出三角形全等的条件,证明△BCE≌ACD′,再利用中位线的性质,等量代换即可得BE=2CF,利用三角形外角定理,等腰三角形性质∠BGF=∠ECG+∠BEC=∠ECG+∠DCF=∠DCE=90°,得BE⊥CF;
(3)利用(2)的结论,利用含30°角直角三角形的性质,锐角三角函数,即平行线分线段成比例定理即可.
解答  (1)解:BE⊥CF,BE=2CF.
(1)解:BE⊥CF,BE=2CF.
理由:∵等腰直角△ABC,
∴BC=AC,∠BCA=90°,
同理:DC=EC,
在△BCE和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD=90°}\\{DC=EC}\end{array}\right.$,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠CBE=∠CAD,
点D为线段AD的中点,∠BCA=90°,
∴CF=AF=$\frac{1}{2}$AD,
∴BE=2CF,∠ACF=∠CAD,
∴∠ACF=∠CBE,
设BE与CF交于点G,
则∠EGF=∠BCF+∠CBE=∠BCF+∠ACF=∠ACB=90°,
∴BE⊥CF,
故答案为:BE=2CF,BE⊥CF.
(2)解:(1)中的关系仍然成立.
理由:如图2,延长DC至D′,使CD′=CD,
∵等腰直角△DCE,∴CE=CD=CD′,∠3=∠DCE=90°
同理:BC=AC,∠BCA=90;
∵∠1=∠2=α,
∴∠1+∠DCE=∠2+∠3,∠BCE=∠ACD′,
在△BCE和△ACD′中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD′}\\{CE=CD′}\end{array}\right.$,
∴△BCE≌ACD′(SAS),
∵点F为线段AD的中点,CD′=CD,
∴AD′=2CF,CF∥AD′,
∴BE=2CF,∠DCF=∠D′,
∴∠BEC=∠DCF,
∴∠ACF=∠CBE,∠ACF=∠CAD,
设BE与CF交于点G,
则∠BGF=∠ECG+∠BEC=∠ECG+∠DCF=∠DCE=90°,
∴BE⊥CF.
(3)解:设BE与CF交于点G,
∵∠DCE=90°,∠DCF=30°,
∴∠GCE=60°,
∵BE⊥CF,
∴∠MGC=∠EGC=90°,
设MG=x,
在Rt△CMG中,∠DCF=30°,
∴$CM=2x,CG=\sqrt{3}$x.
在Rt△CEG中,∠GCE=60°,
∴CE=2$\sqrt{3}$x,EG=3x,
∴$CD=CE=2\sqrt{3}x$,ME=MG+EG=x+3x=4x,
∴DM=CD-CM=2$\sqrt{3}$x-2x=(2$\sqrt{3}$-2)x,
∵等腰直角△DCE,
∴∠CDE=45°,
∵∠BCD=45°,
∴∠CDE=∠BCD,
∴DE∥BC,
∴$\frac{CM}{BM}$=$\frac{DM}{EM}$=$\frac{(2\sqrt{3}-2)x}{4x}$=$\frac{\sqrt{3}-1}{2}$
点评 本题考查等腰三角形性质,全等三角形性质及判定,直角三角形性质及平行线分线段成比例定理的综合运用,找出全等条件,构建全等三角形是解决此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 小红家、小刚家、科技馆依次在同一条公路旁.小红与小刚同时从自家出发步行去科技馆,始终保持匀速行走,并先后到达.两人与小刚家的距离y(米)与行走时间x(分)之间的函数关系如图所示.下列四个结论,其中正确的有( )
小红家、小刚家、科技馆依次在同一条公路旁.小红与小刚同时从自家出发步行去科技馆,始终保持匀速行走,并先后到达.两人与小刚家的距离y(米)与行走时间x(分)之间的函数关系如图所示.下列四个结论,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3)3•(-3)4=-37 | B. | (-28)3=(-2)24 | C. | (3×105)2=9×1010 | D. | ${({-3})^5}÷{3^6}=-\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
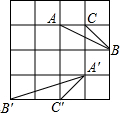 如图是一个边长为1的正方形组成的网络,△ABC和△A′B′C′都是格点三角形,请问△ABC和△A′B′C′是否相似?答:相似;若相似,它们的相似比等于$\frac{\sqrt{2}}{2}$.
如图是一个边长为1的正方形组成的网络,△ABC和△A′B′C′都是格点三角形,请问△ABC和△A′B′C′是否相似?答:相似;若相似,它们的相似比等于$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
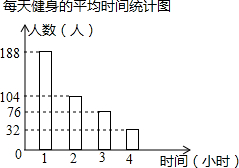 某学习小组想了解某县每个居民一天的平均健身时间,准备采用以下调查方式中的一种进行调查:
某学习小组想了解某县每个居民一天的平均健身时间,准备采用以下调查方式中的一种进行调查:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com