
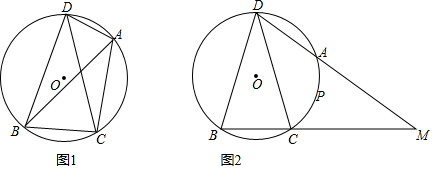
分析 (1)如图1中,只要证明∠DBC=∠3即可解决问题;
(2)如图2中,作PF⊥BM于F,PE⊥DM于E,连接PD、PM、PC、PA.首先证明MA=MC,作AH⊥CM于H,由tan∠AMC=$\frac{3}{4}$=$\frac{AH}{HM}$,设AH=3k,HM=4k,则AM=CM=5k,CF=k,推出tan∠ACH=$\frac{AH}{CH}$=$\frac{3k}{k}$=3,由∠CAM=∠DBC=∠DCB=∠ACB,可得tan∠DCB=3.
解答 (1)证明:如图1中,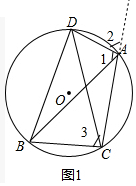
∵∠2+∠DAC=180°,∠DBC+∠DAC=180°,
∴∠2=∠DBC,
∵∠1=∠3,∠1=∠2,
∴∠DBC=∠3,
∴DB=DC.
(2)解:如图2中,作PF⊥BM于F,PE⊥DM于E,连接PD、PM、PC、PA.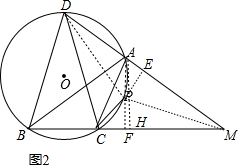
∵P是△DCM的内心,
∴∠PMA=∠PMC,∠PDA=∠PDC,
∴PE=PF,PA=PC,
易证△PEA≌△PFC,△PEM≌△PFM,
∴AE=CF,EM=FM,
∴AM=CM,
作AH⊥CM于H,
∵tan∠AMC=$\frac{3}{4}$=$\frac{AH}{HM}$,
设AH=3k,HM=4k,则AM=CM=5k,CF=k,
∴tan∠ACH=$\frac{AH}{CH}$=$\frac{3k}{k}$=3,
∵∠CAM=∠DBC=∠DCB=∠ACB,
∴tan∠DCB=3.
点评 本题考查三角形的内心、圆周角定理、等腰三角形的判定和性质、勾股定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
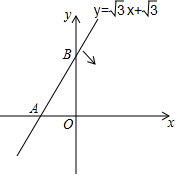 如图示直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,当直线绕着点A按顺时针方向旋转到与x轴首次重合时,点B运动的路径的长度为$\frac{2}{3}$π.
如图示直线y=$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,当直线绕着点A按顺时针方向旋转到与x轴首次重合时,点B运动的路径的长度为$\frac{2}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
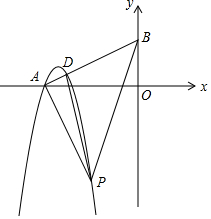 已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t取任何符合条件的实数,点A,P都在抛物线C 上.
已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t取任何符合条件的实数,点A,P都在抛物线C 上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
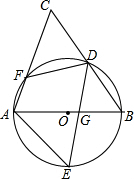 如图,AB是圆O的直径,D、E为圆心O上位于AB异侧的两点,连接BD并延长至点C,连接AC交圆心O于点F,连接AE、DE、DF,已知∠E=∠C.
如图,AB是圆O的直径,D、E为圆心O上位于AB异侧的两点,连接BD并延长至点C,连接AC交圆心O于点F,连接AE、DE、DF,已知∠E=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
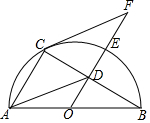 如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
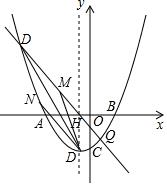 抛物线y=$\frac{1}{3}$x2+bx+c经过点A(-4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.
抛物线y=$\frac{1}{3}$x2+bx+c经过点A(-4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com