Question

“石头、剪子、布”是一个广为流传的游戏、规则是：甲、乙都做出“石头”、“剪子”、“布”三种手势中的一种，规定“石头”胜“剪子”，“剪子”胜“布”，“布”胜“石头”，手势相同不分胜负．假定甲、乙两人每次都是随意并且同时做出三种手势中的一种，那么
（1）甲取胜的概率是多少？
（2）乙取胜的概率是多少？
（3）甲、乙不分胜负的概率是多少？请画出树状图或列表加以计算．

Answer 1

分析：先根据题意列出可能出现的情况，再分别找出甲赢、乙赢及甲、乙不分胜负的情况，由概率公式分别求出各种情况出现的概率即可．

解答：解：设甲赢为事件A，乙赢的事件为B，不分胜负的事件为C
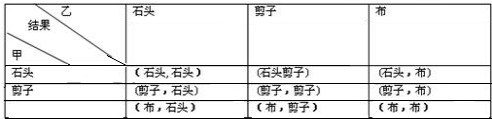
有表格可知，共出现的情况有9种，
（1）甲胜的情况为（石头，剪子），（剪子，布），（布，石头）三种情况，
所以甲胜的概率为P（A）=

3

9

=

1

3

；
（2）乙胜的情况为（石头，剪子），（剪子，布），（布，石头）三种情况，
所以乙胜的概率为P（B）=

3

9

=

1

3

；
（3）甲、乙不分胜负的情况为（石头，石头），（剪子，剪子），（布，布），
故甲乙不分胜负的概率为P（C）=

3

9

=

1

3

．
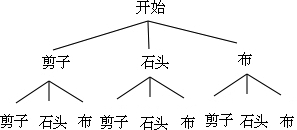
画树状图得：

点评：本题考查的是用列举法求概率，解答此题的关键是列出可能出现的所有情况，用到的知识点为：概率=所求情况数与总情况数之比．