练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知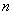是正整数,则奇数可以用代数式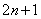来表示.

    (1)分解因式: ;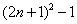

    (2)我们把所有”奇数的平方减去1”所得的数叫”白银数”,则所有”白银数”的最大公约数是多少?请简要说明理由.


    解: (1)

    (2) 所有”白银数”的最大公约数是8

    ∵n正整数,则n与n+1必有一个偶数,∴n(n+1)必是2的倍数,则4n(n+1)必是8的倍数,

    ∴所有”白银数”的最大公约数是8……………2分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知直线AC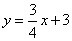： 与直线BC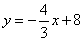：相交于点C，分别交x轴于点A、B，P为x轴上的一点，设P（m,0），以点P为圆心作圆：

    （1）若－4<m <6.当m=______时，⊙P同时与AC、BC相切；

    （2）设⊙P的半径为3，当m=_______时，⊙P与直线AC、直线BC中的一条相切。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式x(x+4)+4的结果              ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一次函数，若随的增大而增大，则的值可以是（    ）

    （A）1       （B）2      （C）3      （D）4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    数据1、5、6、5、6、5、6、6的众数是          ，方差是        ． 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    点A（-1,0）B（4,0）C（0,2）是平面直角坐标系上的三点。

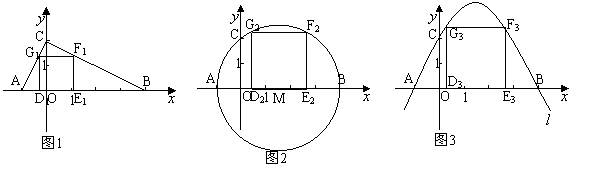
    ① 如图1先过A、B、C作△ABC，然后在在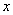轴上方作一个正方形D1E1F1G1,

    使D1E1在AB上， F1、G1分别在BC、AC上

    ② 如图2先过A、B、C作圆⊙M，然后在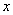轴上方作一个正方形D2E2F2G2,

    使D2E2在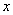轴上 ，F2、G2在圆上

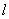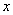    ③ 如图3先过A、B、C作抛物线，然后在轴上方作一个正方形D3E3F3G3,

    使D3E3在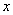轴上， F3、G3在抛物线上

    请比较 正方形D1E1F1G1 , 正方形D2E2F2G2 , 正方形D3E3F3G3 的面积大小

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知扇形的圆心角为60°，半径为1，则扇形的弧长为（　　）

    　

    A．

    B．

    π

    C．

    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    数学活动﹣求重叠部分的面积

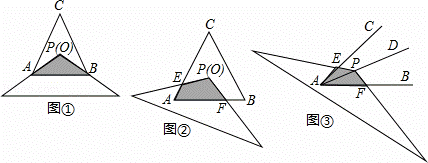
    （1）问题情境：如图①，将顶角为120°的等腰三角形纸片（纸片足够大）的顶点P与等边△ABC的内心O重合，已知OA=2，则图中重叠部分△PAB的面积为　　．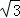

    （2）探究1：在（1）的条件下，将纸片绕P点旋转至如图②所示位置，纸片两边分别与AC，AB交于点E，F，图②中重叠部分的面积与图①重叠部分的面积是否相等？如果相等，请给予证明；如果不相等，请说明理由．

    （3）探究2：如图③，若∠CAB=α（0°＜α＜90°），AD为∠CAB的角平分线，点P在射线AD上，且AP=2，以P为顶点的等腰三角形纸片（纸片足够大）与∠CAB的两边AC，AB分别交于点E、F，∠EPF=180°﹣α，求重叠部分的面积．（用α或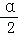的三角函数值表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=2，则图中阴影部分的面积为　．

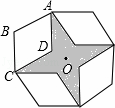
    查看答案和解析>>

    同步练习册答案