
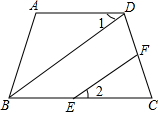
 ��������������̣�
��������������̣����� �����A+��ABC=180�㣬����ƽ���ߵ��ж��ó�AD��BC������ƽ���ߵ����ʵó���1=��DBC�����ݴ�ֱ�ó���BDF=��EFC=90�㣬����ƽ���ߵ��ж��ó�BD��EF������ƽ���ߵ����ʵó���2=��DBC�����ɵó��𰸣�
��� ֤�����ߡ�A=106��-������ABC=74��+������֪����
���A+��ABC=180�㣬
��AD��BC��ͬ���ڽǻ�������ֱ��ƽ�У���
���1=��DBC����ֱ��ƽ�У��ڴ������ ����
��BD��DC��EF��DC����֪����
���BDF=��EFC=90�㣨��ֱ�Ķ��壩��
��BD��EF��ͬλ����ȣ���ֱ��ƽ�У���
���2=��DBC����ֱ��ƽ�У�ͬλ����ȣ���
���1=��2��������������
�ʴ�Ϊ��BC��ͬ���ڽǻ�������ֱ��ƽ�У���DBC����ֱ�Ķ��壬EF��ͬλ����ȣ���ֱ��ƽ�У���DBC����ֱ��ƽ�У�ͬλ����ȣ�����������
���� ���⿼����ƽ���ߵ����ʺ��ж�����ƽ���߶����֪ʶ�㣬��������ö������������ǽ����Ĺؼ���ע�⣺ƽ���ߵ������У�����ֱ��ƽ�У�ͬλ����ȣ�����ֱ��ƽ�У��ڴ�����ȣ�����ֱ��ƽ�У�ͬ���ڽǻ�������֮��Ȼ��


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
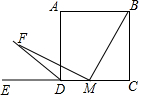 ��ͼ����������ABCD�У�AB=2����MΪ������ABCD�ı�CD�ϵĶ��㣨���C��D���غϣ�������BM����MF��BM����������ABCD����ǡ�ADE��ƽ���߽��ڵ�F����CM=x����DFM�����Ϊy����y��x֮��ĺ�����ϵʽy=-$\frac{1}{2}$x2+x��
��ͼ����������ABCD�У�AB=2����MΪ������ABCD�ı�CD�ϵĶ��㣨���C��D���غϣ�������BM����MF��BM����������ABCD����ǡ�ADE��ƽ���߽��ڵ�F����CM=x����DFM�����Ϊy����y��x֮��ĺ�����ϵʽy=-$\frac{1}{2}$x2+x���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
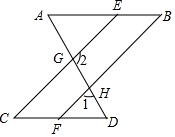 ��ͼ����֪��A=��AGE����D=��DGC��
��ͼ����֪��A=��AGE����D=��DGC���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com