
分析 (1)根据两个抛物线的顶点关于原点对称,即可解决问题;
(2))因为抛物线l1:y=a(x-1)2+2经过原点,可得a=-2,推出抛物线l2的解析式为y=2(x+1)2-2,令y=0,2(x+1)2-2=0,解得x=0或-2,推出D(-2,0),C(0,0);
(3)由题意可知A($\frac{3}{2}$,0),B($\frac{1}{2}$,0),C(-$\frac{1}{2}$,0),D(-$\frac{3}{2}$,0),把B($\frac{1}{2}$,0)代入y=a(x-1)2+2即可解决问题.
(4)①设t秒后,B、C两点再次成为AD的三等分点.列出方程即可解决问题.
②如图,由①可知,抛物线l1:y=-8(x-$\frac{1}{2}$)2+2,抛物线l2的解析式为y=8x2-2,由PQ=2,P[m,-8(m-$\frac{1}{2}$)2+2],Q(m,8m2-2),推出|8m2-2-[-8(m-$\frac{1}{2}$)2+2]|=2,解方程即可解决问题.
解答 解:(1)∵抛物线l2与抛物线l1关于原点对称,
∴抛物线l2的顶点N与抛物线l1关的顶点M(1,2)关于原点对称,
∴N(-1,-2).
故答案为(-1,-2);
(2)∵抛物线l1:y=a(x-1)2+2经过原点,
∴0=a+2,
∴a=-2,
∴抛物线l2的解析式为y=2(x+1)2-2,
令y=0,2(x+1)2-2=0,解得x=0或-2,
∴D(-2,0),C(0,0),
∴a=-2,D(-2,0);
(3)∵A、B、C、D四点从右到做左依次排列,且B、C两点是线段AD的三等分点,
又∵抛物线的对称轴分别为x=-1和x=1,
∴A($\frac{3}{2}$,0),B($\frac{1}{2}$,0),C(-$\frac{1}{2}$,0),D(-$\frac{3}{2}$,0),
把B($\frac{1}{2}$,0)代入y=a(x-1)2+2得到a=-8,
∴a=-8.
(4)①设t秒后,B、C两点再次成为AD的三等分点.
由(2)可知,A($\frac{3}{2}$,0),B($\frac{1}{2}$,0),C(-$\frac{1}{2}$,0),D(-$\frac{3}{2}$,0),
由题意:此时CA=$\frac{1}{3}$AD,即2-3t=$\frac{1}{3}$(3-3t),解得t=$\frac{1}{2}$,
∴t=$\frac{1}{2}$秒时,B、C两点再次成为AD的三等分点.
②如图,由①可知,抛物线l1:y=-8(x-$\frac{1}{2}$)2+2,抛物线l2的解析式为y=8x2-2,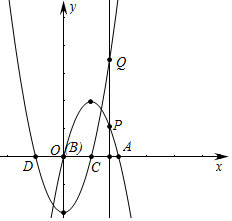
∵PQ=2,P[m,-8(m-$\frac{1}{2}$)2+2],Q(m,8m2-2),
∴|8m2-2-[-8(m-$\frac{1}{2}$)2+2]|=2,
解得m=0或$\frac{1}{2}$或$\frac{1+\sqrt{5}}{4}$或$\frac{1-\sqrt{5}}{4}$.
点评 本题考查二次函数综合题、平移变换、中心对称等知识,解题的关键是理解题意,学会用方程的思想思考问题,属于中考压轴题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求:
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
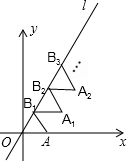 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2017的坐标是(2017,2017$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2017的坐标是(2017,2017$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
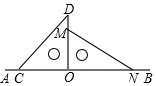 如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周,在旋转的过程中,当第5.5或11.5秒时,直线CD恰好与直线MN垂直.
如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周,在旋转的过程中,当第5.5或11.5秒时,直线CD恰好与直线MN垂直.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com