
【题目】在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.

(1)求抛物线的解析式;
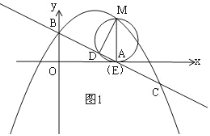
(2)如图,横坐标为![]() 的点
的点![]() 在直线
在直线![]() 上方的抛物线上,过点
上方的抛物线上,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以
,以![]() 为直径的圆交直线
为直径的圆交直线![]() 于另一点
于另一点![]() .当点
.当点![]() 在
在![]() 轴上时,求
轴上时,求![]() 的周长;
的周长;
(3)将![]() 绕坐标平面内的某一点按顺时针方向旋转
绕坐标平面内的某一点按顺时针方向旋转![]() ,得到
,得到![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() .若
.若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+1;
x+1;
(2)△DEM的周长=![]() ;
;
(3)点A1(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用待定系数法求抛物线的解析式;
(2)如图1,A与E重合,根据直线y=﹣![]() x+1求得与x轴交点坐标可得OA的长,由勾股定理得AB的长,利用等角的三角函数得:sin∠ABO=
x+1求得与x轴交点坐标可得OA的长,由勾股定理得AB的长,利用等角的三角函数得:sin∠ABO=![]() ,cos∠ABO=
,cos∠ABO=![]() ,则可得DE和DM的长,根据M的横坐标代入抛物线的解析式可得纵坐标,即ME的长,相加得△DEM的周长;
,则可得DE和DM的长,根据M的横坐标代入抛物线的解析式可得纵坐标,即ME的长,相加得△DEM的周长;
(3)由旋转可知:O1A1⊥x轴,O1B1⊥y轴,设点A1的横坐标为x,则点B1的横坐标为x+1,所以点O1,A1不可能同时落在抛物线上,分以下两种情况:
①如图2,当点O1,B1同时落在抛物线上时,根据点O1,B1的纵坐标相等列方程可得结论;
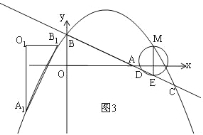
②如图3,当点A1,B1同时落在抛物线上时,根据点B1的纵坐标比点A1的纵坐标大![]() ,列方程可得结论.
,列方程可得结论.
试题解析:(1)∵直线y=﹣![]() x+1交y轴于点B,∴B(0,1),
x+1交y轴于点B,∴B(0,1),
∵抛物线y=﹣![]() x2+bx+c经过点B和点C(4,﹣2).∴
x2+bx+c经过点B和点C(4,﹣2).∴![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+1;
x+1;
(2)如图1,∵直线y=﹣![]() x+1交x轴于点A,
x+1交x轴于点A,
当y=0时,﹣![]() x+1=0,x=
x+1=0,x=![]() ,∴A(
,∴A(![]() ,0),∴OA=
,0),∴OA=![]() ,
,
在Rt△AOB中,∵OB=1,∴AB=![]() ,∴sin∠ABO=
,∴sin∠ABO=![]() ,cos∠ABO=
,cos∠ABO=![]() ,
,
∵ME∥x轴,
∴∠DEM=∠ABO,
∵以ME为直径的圆交直线BC于另一点D,
∴∠EDM=90°,
∴DE=MEcos∠DEM=![]() ME,DM=MEsin∠DEM=
ME,DM=MEsin∠DEM=![]() ME,
ME,
当点E在x轴上时,E和A重合,则m=OA=![]() ,
,
当x=![]() 时,y=﹣
时,y=﹣![]() ×(
×(![]() )2+
)2+![]() ×
×![]() +1=
+1=![]() ;∴ME=
;∴ME=![]() ,
,
∴DE=![]() =
=![]() ,DM=
,DM=![]() =
=![]() ,
,
∴△DEM的周长=DE+DM+ME=![]() =
=![]() ;
;
(3)由旋转可知:O1A1⊥x轴,O1B1⊥y轴,设点A1的横坐标为x,则点B1的横坐标为x+1,
∵O1A1⊥x轴,
∴点O1,A1不可能同时落在抛物线上,分以下两种情况:
①如图2,当点O1,B1同时落在抛物线上时,
点O1,B1的纵坐标相等,
∴﹣![]() x2+
x2+![]() x+1=﹣
x+1=﹣![]() (x+1)2+
(x+1)2+![]() (x+1)+1,
(x+1)+1,
解得:x=![]() ,
,
此时点A1的坐标为(![]() ,
,![]() ),
),
②如图3,当点A1,B1同时落在抛物线上时,
点B1的纵坐标比点A1的纵坐标大![]() ,
,
﹣![]() x2+
x2+![]() x+1+
x+1+![]() =﹣
=﹣![]() (x+1)2+
(x+1)2+![]() (x+1)+1,
(x+1)+1,
解得:x=﹣![]() ,
,
此时A1(﹣![]() ,
,![]() ),
),
综上所述,点A1(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).



科目:初中数学 来源: 题型:
【题目】下列命题中:正确的说法有
①两个全等三角形合在一起是一个轴对称图形;
②成轴对称的两个图形一定全等;
③直线l经过线段AB的中点,则l是线段AB的垂直平分线;
④一条线段可以看作是以它的垂直平分线为对称轴的轴对称图形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).
A.中位数B.众数C.平均数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(8x3﹣12x2﹣4x)÷(﹣4x)=( )
A. ﹣2x2+3xB. ﹣2x2+3x+1C. ﹣2x2+3x﹣1D. 2x2+3x+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一个新运算,若i1=i,i2=﹣1,i3=﹣i,i4=1,i5=i,i6=﹣1,i7=﹣i,i8=1,…,则i2020=( )
A.﹣iB.iC.﹣1D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不能进行平方差计算的是( )
A.(x+y)(﹣x﹣y)
B.(2a+b)(2a﹣b)
C.(﹣3x﹣y)(﹣y+3x)
D.(a2+b)(a2﹣b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com