
 已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E.
已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E. 证明:(1)∵AC与小圆O相切于点C,
证明:(1)∵AC与小圆O相切于点C,分析:
(1)欲证BD是小圆的切线,只需证明∠OBD=90°(或BD⊥OB)即可;
(2)由(1)中全等三角形△AOC≌△DOB的性质、切线BD的性质推知△ABE∽△DBO;然后根据相似三角形的对应边成比例求得BE:AE=OB:OD;由小圆的两条切线CE=BE,小圆的半径OC=OB可以证得结论.
点评:本题考查了切线的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质.注意,切线性质是:圆的切线垂直于经过切点的“半径”.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
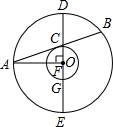 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB和小圆相切于点C,过点C作大圆的弦DE,使DE⊥OA,垂足为F,DE交小圆于另一点G.求证:AF•AO=DC•DG.
已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB和小圆相切于点C,过点C作大圆的弦DE,使DE⊥OA,垂足为F,DE交小圆于另一点G.求证:AF•AO=DC•DG.查看答案和解析>>
科目:初中数学 来源: 题型:
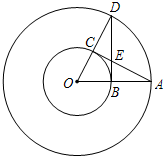 (2006•上海模拟)已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E.
(2006•上海模拟)已知:如图,在以点O为圆心的两个同心圆中,大圆的半径OA与小圆相交于点B,AC与小圆相切于点C,OC的延长线与大圆相交于点D,AC与BD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1998•四川)已知:如图,在以O 为圆心的两个同心圆中,大圆O的内接四边形ABCD的边AB切小圆O于点P,两条对角线AC、BD相交于点Q,AQ和AD的长是方程x2-7x+12=0的两根,小圆O的半径等于CD长的一半,AK是大圆的直径.
(1998•四川)已知:如图,在以O 为圆心的两个同心圆中,大圆O的内接四边形ABCD的边AB切小圆O于点P,两条对角线AC、BD相交于点Q,AQ和AD的长是方程x2-7x+12=0的两根,小圆O的半径等于CD长的一半,AK是大圆的直径.查看答案和解析>>
科目:初中数学 来源:2006年上海市部分学校初三数学抽样测试卷(5月份)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com