
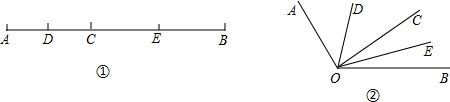
分析 (1)根据线段中点的性质计算即可;
(2)根据线段中点的性质和给出的数据,结合图形计算;
(3)同(1)的解法相同;
(4)根据角平分线的定义进行解答即可.
解答 解:(1)∵点D,E分别是AC和BC的中点,
∴DC=$\frac{1}{2}$AC,CE=$\frac{1}{2}$CB,
∴DC+CE=$\frac{1}{2}$(AC+CB)=6cm;
故答案为:6.
(2)∵AC=4cm,
∴CD=2cm,
∵AB=12cm,AC=4cm,
∴BC=8cm,
∴CE=4cm,DE=DC+CE=6cm;
(3))∵点D,E分别是AC和BC的中点,
∴DC=$\frac{1}{2}$AC,CE=$\frac{1}{2}$CB,
∴DC+CE=$\frac{1}{2}$(AC+CB),
即DE=$\frac{1}{2}$AB;
(4)∵OD,OE分别平分∠AOC和∠BOC,
∴∠DOC=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠COB,
∴∠DOE=∠DOC+∠COE=$\frac{1}{2}$∠AOB=50°,
当∠AOB=n°,∠DOE=$\frac{1}{2}$n°.
故答案为:50;$\frac{1}{2}$n.
点评 本题考查的是线段的计算和角的计算,掌握线段中点的性质和角平分线的定义是解题的关键,注意类比思想的应用.


科目:初中数学 来源: 题型:解答题
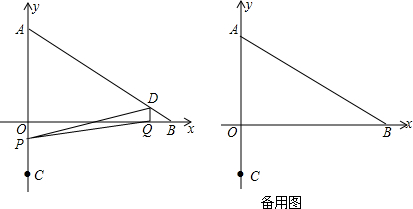
 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限内,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示:抛物线y=ax2+ax-5经过点B.
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限内,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示:抛物线y=ax2+ax-5经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a=b,则a+c=b+c | B. | 若a+c=b+c,则a=b | C. | 若a=b,则ac=bc | D. | 若ac=bc,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com