练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，ΔABC中，AD是高，AE、BF是角平分线，它们相交与点O，∠BAC=50°，∠C=70°，则∠DAC的度数为__________，∠BOA的度数为__________．

    【答案】20° 125°

    【解析】

    因为AD是高，所以∠ADC=90°，又因为∠C=70°，所以∠DAC度数可求；因为∠BAC=50°，∠C=70°，所以∠BAO=25°，∠ABC=60°，BF是∠ABC的角平分线，则∠ABO=30°，故∠BOA的度数可求．

    ∵AD⊥BC，∴∠ADC=90°

    ∵∠C=70°，∴∠DAC=180°﹣90°﹣70°=20°；

    ∵∠BAC=50°，∠C=70°，∴∠BAO=25°，∠ABC=180°-∠C-∠BAC=60°．

    ∵BF是∠ABC的角平分线，∴∠ABO=30°，∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°．

    故答案为：20°，125°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下面的材料并解答后面的问题：

    （阅读）

    小亮：你能求出x2+4x﹣3的最小值吗？如果能，其最小值是多少？

    小华：能．求解过程如下：

    因为x2+4x﹣3＝x2+4x+4﹣4﹣3＝（x2+4x+4）﹣（4+3）＝（x+2）2﹣7．

    而（x+22）≥0，所以x2+4x﹣3的最小值是﹣7．

    （1）小华的求解过程正确吗？

    （2）你能否求出x2﹣5x+4的最小值？如果能，写出你的求解过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个多边形的所有内角与它的一个外角之和是2018°，求这个外角的度数和它的边数．

    【答案】38° ； 边数13

    【解析】试题分析：根据多边形的内角和公式（n-2）180°可知，多边形的内角和是180°的倍数，然后列式求解即可．

    试题解析：设多边形的边数是n，加的外角为α，则

    （n-2）180°+α=2018°，

    α=2378°-180°n，又0＜α＜180°，

    即0＜2378°-180°n＜180°，

    解得： ＜n＜，

    又n为正整数，

    可得n=13，

    此时α=38°满足条件，

    答：这个外角的度数是38°，它的13边形．

    【点睛】本题考查了多边形的内角和公式，利用好多边形的内角和是180°的倍数是解题的关键．

    【题型】解答题
    【结束】
    22

    【题目】已知, 求 (1) ； (2) .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】ΔABC、ΔCDE都是等边三角形，AD、BE相交于点O，点M、点N分别是线段AD、BE的中点.

    （1）证明： AD=BE.（2）求∠DOE的角度。（3）证明：ΔMNC是等边三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中,正确的个数为(　　)

    ①三角形的三条高都在三角形内,且都相交于一点

    ②三角形的中线都是过三角形的某一个顶点,且平分对边的直线

    ③在△ABC中,若,则△ABC是直角三角形

    ④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2＜b＜18.

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，ACB和DCE都是等腰直角三角形，∠ACB=∠DCE=90，连接AE、BD交于点O. AE与DC交于点M，BD与AC交于点N.

    （1）如图①，求证：AE=BD；

    （2）如图②，若AC=DC，在不添加任何辅助线的情况下，请直接写出图②中四对全等的直角三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

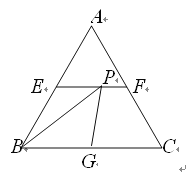
    【题目】如图所示，在边长为2的正三角形ABC中，E、F、G分别为AB、

    AC、BC的中点，点P为线段EF上一个动点，连接BP、GP，则△BPG的周长的最小值是

    _ ▲ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y=ax2+4x+c与y轴交于点A（0，5），与x轴交于点E，B，点B坐标为（5，0）．

    （1）求二次函数解析式及顶点坐标；

    （2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，直线l1与x轴、y轴分别交于点A（3，0）、B（0，2）．

    （1）如图2，点M是AB的中点，过点M作ME⊥x轴，MF⊥y轴，垂足分别为E、F．则点M 的坐标为 ；

    （2）如图3，直线l2经过点B，且与l1互相垂直，过点C（0，﹣1）作CD⊥y轴，交l2于点D．则以直线l2为图像的函数表达式为 ；

    （3）图1中，在x轴上是否存在点P，使得△APB是等腰三角形．如果存在，请求出点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案