
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

【答案】(1)见解析(2)成立(3)△DEF为等边三角形
【解析】解:(1) 证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=900。
∵∠BAC=900,∴∠BAD+∠CAE=900。
∵∠BAD+∠ABD=900,∴∠CAE=∠ABD。
又AB=AC ,∴△ADB≌△CEA(AAS)。∴AE=BD,AD=CE。
∴DE=AE+AD= BD+CE。
(2)成立。证明如下:
∵∠BDA =∠BAC=![]() ,∴∠DBA+∠BAD=∠BAD +∠CAE=1800—
,∴∠DBA+∠BAD=∠BAD +∠CAE=1800—![]() 。∴∠DBA=∠CAE。
。∴∠DBA=∠CAE。
∵∠BDA=∠AEC=![]() ,AB=AC,∴△ADB≌△CEA(AAS)。∴AE=BD,AD=CE。
,AB=AC,∴△ADB≌△CEA(AAS)。∴AE=BD,AD=CE。
∴DE=AE+AD=BD+CE。
(3)△DEF为等边三角形。理由如下:
由(2)知,△ADB≌△CEA,BD=AE,∠DBA =∠CAE,
∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=600。
∴∠DBA+∠ABF=∠CAE+∠CAF。∴∠DBF=∠FAE。
∵BF=AF,∴△DBF≌△EAF(AAS)。∴DF=EF,∠BFD=∠AFE。
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600。
∴△DEF为等边三角形。
(1)因为DE=DA+AE,故由AAS证△ADB≌△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE。
(2)成立,仍然通过证明△ADB≌△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD。
(3)由△ADB≌△CEA得BD=AE,∠DBA =∠CAE,由△ABF和△ACF均等边三角形,得∠ABF=∠CAF=600,FB=FA,所以∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠FAE,所以△DBF≌△EAF,所以FD=FE,∠BFD=∠AFE,再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF是等边三角形。


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门 步而见木.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)、菱形![]() 的边长1,面积为
的边长1,面积为![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
(2)、如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC=

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积.
(2)在图形中作出△ABC关于x轴的对称图形△A1B1C1.写出点A1,B1,C1的坐标.
(3)在图形中作出△ABC关于y轴的对称图形△A2B2C2.写出点A2,B2,C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
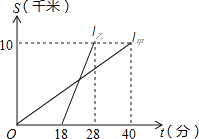
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,直线
,直线![]() 和直线
和直线![]() 交于点C、D,直线
交于点C、D,直线![]() 上有一点P.
上有一点P.
(1)如图1,点P在C、D之间运动时,∠PAC、∠APB、∠PBD之间有什么关系?并说明理由。
(2)若点P在C、D两点外侧运动时(P点与C、D不重合,如图2、3),试直接写出∠PAC、∠APB、∠PBD之间有什么关系,不必写理由。

图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com