
| A. | 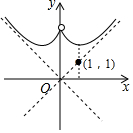 | B. | 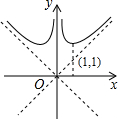 | C. |  | D. | 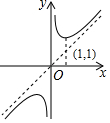 |
分析 本题可用排除法解答,根据y始终大于0,可排除D,再根据x的绝对值越接近于0(如x=±0.1,或x=±0.01)时,每个图象两侧都是无限上升,可排除A,根据函数y=$\frac{{x}^{2}+1}{|x|}$和y=$\frac{3}{2}$x有交点即可排除C,即可解题.
解答 解:x取±1,±2,±3,会发现最小值是x取±1时y=2,由此选项C,D错误;
x的绝对值越接近于0(如x=±0.1,或x=±0.01)时,每个图象两侧都是无限上升,可排除A,
∵当直线经过(0,0)和(1,1)时,直线解析式为y=x,
当y=x=$\frac{{x}^{2}+1}{|x|}$时,x无解,
∴y=x与y=$\frac{{x}^{2}+1}{|x|}$没有有交点,∴B正确;
故选B.
点评 此题主要考查了函数图象的性质,考查了平方根和绝对值大于等于0的性质,本题中求得直线与函数的交点是解题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:
“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.
如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩x 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 | 1 | 0 | 0 | 7 | 10 | 2 |
| 部门 | 平均数 | 中位数 | 众数 |
| 甲 | 78.3 | 77.5 | 75 |
| 乙 | 78 | 80.5 | 81 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com