
【题目】在平面直角坐标系中,点A(1,1),B(4,3),将点A向左平移2个单位长度,再向上平移3个单位长度得到点C.
(1)写出点C的坐标;
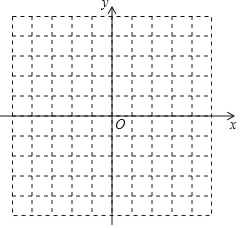
(2)画出△ABC并判断△ABC的形状.
【答案】(1)C(﹣1,4);(2)△ABC是等腰直角三角形;过程见详解.
【解析】
(1)根据向左平移2个单位长度为横坐标减2,向上平移3个单位长度为纵坐标加3,即可得到C点坐标.
(2)如图,顺次连接A,B,C,然后根据每个点的坐标利用两点间的距离公式分别求出AB,BC,CA的长,再根据勾股定理逆定理判断即可.
(1)∵将点A(1,1)向左平移2个单位长度,再向上平移3个单位长度得到点C,
∴C(﹣1,4);
(2)△ABC是等腰直角三角形;
如图所示,根据勾股定理得,AB=![]() =
=![]() =
=![]() ,
,
BC=![]() =
=![]() =
=![]() ,
,
AC=![]() =
=![]() =
=![]() ,
,
∴AB=AC,
∵AB2+AC2=BC2=26,
∴△ABC是直角三角形,
∴△ABC是等腰直角三角形.



科目:初中数学 来源: 题型:
【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的![]() (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某地有一地下工程,其底面是正方形,面积为405m2,四个角是面积为5m2的小正方形渗水坑,根据这些条件如何求a的值?与你的同伴进行交流.
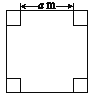
下面是小康提供的解题方案,根据解题方案请你完成本题的解答过程:
①设大正方形的边长为x m,小正方形的边长为y m,那么根据题意可列出关于x的方程为_______,关于y的方程为_______;
②利用平方根的意义,可求得x=________(取正值,结果保留根号),y=________(取正值,结果保留根号);
③所以a=x-2y=____________=__________(结果保留根号);
④答:________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与x轴相交于点B(1,0)和点C(9,0)两点,与y轴的负半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴正半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.
(1)求点A坐标和⊙P的半径;
(2)求抛物线的解析式;
(3)当△MOB与以点B、C、D为顶点的三角形相似时,求△CDN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率. 
查看答案和解析>>
科目:初中数学 来源: 题型:
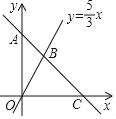
【题目】一次函数y=kx+b的图象经过点A(0,9),并且与直线y=![]() x相交于点B,与x轴相交于点C.
x相交于点B,与x轴相交于点C.
(1)若点B的横坐标为3,求B点的坐标和k,b的值;
(2)在y轴上是否存在这样的点P,使得以点P,B,A为顶点的三角形是等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.
(3)在直线y=kx+b上是否存在点Q,使△OBQ的面积等于![]() ?若存在,请求出点Q的坐标;若不存在,请说明理由.
?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( ) 
A.150°
B.210°
C.105°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个两位正整数,a表示十位上的数字,b表示个位上的数字(a≠b,ab≠0),则这个两位数用多项式表示为 (含a、b的式子);若把十位、个位上的数字互换位置得到一个新两位数,则这两个两位数的和一定能被 整除,这两个两位数的差一定能被 整除
(2)一个三位正整数F,各个数位上的数字互不相同且都不为0.若从它的百位、十位、个位上的数字中任意选择两个数字组成6个不同的两位数.若这6个两位数的和等于这个三位数本身,则称这样的三位数F为“友好数”,例如:132是“友好数”
一个三位正整数P,各个数位上的数字互不相同且都不为0,若它的十位数字等于百位数字与个位数字的和,则称这样的三位数P为“和平数”
①直接判断123是不是“友好数”?
②直接写出共有 个“和平数”
③通过列方程的方法求出既是“和平数”又是“友好数”的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com