
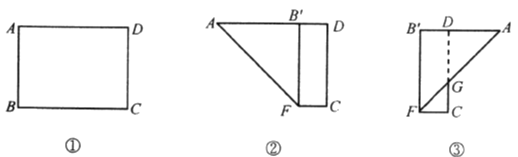
【题目】如图①,在长方形![]() 中,
中,![]() cm,
cm,![]() cm.现将其按下列步骤折叠:(1)将边
cm.现将其按下列步骤折叠:(1)将边![]() 向边
向边![]() 折叠,使边
折叠,使边![]() 落在边
落在边![]() 上,得到折痕
上,得到折痕![]() ,如图②;(2)将
,如图②;(2)将![]() 沿
沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,如图③.则所得梯形
,如图③.则所得梯形![]() 的周长等于( )
的周长等于( )
A. ![]() cm B.
cm B. ![]() cm
cm
C. ![]() cm D.
cm D. ![]() cm
cm
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b﹣ac=4; ④3a﹣c<0.其中正确的个数是( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点. 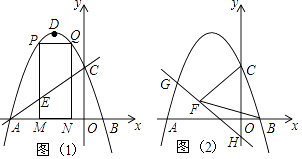
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=__________°;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,∠MAN=60°,射线AM交直线BC于点E,射线AN交直线CD于点F,连结EF,请解答下列问题:
(1)如图1,求证:EC+FC=AC;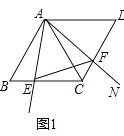
(2)将∠MAN绕点A旋转,如图2,如图3,请直接写出线段EC,FC,AC之间的数量关系,不需要证明;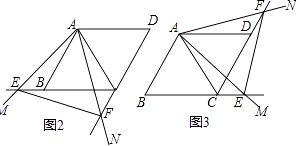
(3)若S菱形ABCD=18 ![]() ,∠CAE=30°,则CF=
,∠CAE=30°,则CF=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com