Question

已知矩形的两对角线所夹的角为60°，且其中一条对角线长为6cm，则该矩形的面积为________．

Answer 1

分析：先画图，由于四边形ABCD是矩形，根据矩形性质可知BD=AC=6，OA=OB，∠ABC=90°，而∠AOB=60°，易证三角形AOB是等边三角形，从而易求∠ACB=30°，也就易求AB，再结合特殊三角函数值可求BC，从而可求矩形面积．
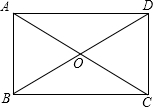
解答：解：如右图所示，∠AOB=60°，AC=6，
∵四边形ABCD是矩形，
∴BD=AC=6，OA=OB，∠ABC=90°，
又∵∠AOB=60°，
∴△AOB是等边三角形，
∴∠ACB=90°-60°=30°，
在Rt△ABC中，AB=AC=3，BC=sin60°•AC=×6=3，
∴S_矩形ABCD=AB×BC=3×3=9．
故答案是9cm²．
点评：本题考查了矩形的性质、等边三角形的判定和性质、矩形的面积、特殊三角形函数值．解题的关键是证明△AOB是等边三角形．注意有一个角等于60°的等腰三角形是等边三角形．