
【题目】如图,![]() 为等腰三角形,顶点
为等腰三角形,顶点![]() 的坐标
的坐标![]() ,底边
,底边![]() 在
在![]() 轴上.将
轴上.将![]() 绕点
绕点![]() 按顺时针方向旋转一定角度后得
按顺时针方向旋转一定角度后得![]() ,点
,点![]() 的对应点
的对应点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的坐标为( )
的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,根据点A的坐标求出OC、AC,再利用勾股定理列式计算求出OA,根据等腰三角形三线合一的性质求出OB,根据旋转的性质可得BO′=OB,∠A′BO′=∠ABO,然后解直角三角形求出O′D、BD,再求出OD,然后写出点O′的坐标即可.
解答:
如图,
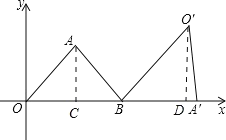
过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,
∵A(2, ![]() ),
),
∴OC=2,AC=![]() ,
,
由勾股定理得,OA=![]() =
=![]() =3,
=3,
∵△AOB为等腰三角形,OB是底边,
∴OB=2OC=2×2=4,
由旋转的性质得,BO′=OB=4,∠A′BO′=∠ABO,
∴O′D=4×![]() =
=![]() ,
,
BD=4×![]() =
=![]() ,
,
∴OD=OB+BD=4+![]() =
=![]() ,
,
∴点O′的坐标为(![]() ,
,![]() ),
),
故答案为C.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
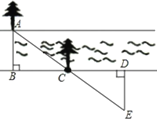
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△ABC中,∠ACB=-90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F
(1)求证:CE=CF.
(2)将图(1)中的△ADE沿AB向右平移到△A’D’E’的位置,使点E’落在BC边上,其它条件不变,如图(2)所示.试猜想:BE'与CF有怎样的数量关系?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
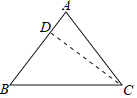
【题目】《几何原本》是一部集前人思想和欧几里得个人创造性于一体的不朽之作,它建立了一套从公理、定义出发,论证命题得到定理的几何学论证方法,形成了一个严密的逻辑体系﹣﹣﹣几何学.以下是《几何原本》第一卷中的命题6,请完成它的证明过程.
命题6:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
已知: .
求证: .
证明:若AB≠AC,其中必有一个较大,不妨设AB>AC,在AB上截取BD=AC,
连接DC.
∵ ,
,
,
∴△ACB≌△DBC
∴∠BDC=∠CAB .
又∠BDC>∠CAB .
∴∠BDC与∠CAB即等于又大于,显然是矛盾的.
∴假设不成立,即AB=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
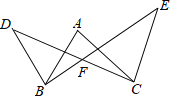
【题目】如图,AB=BD,AC=CE,DC、BE交于点F,∠ABD=∠ACE=60°.
(1)求证:BE=CD;
(2)求∠A+∠ABF+∠ACF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
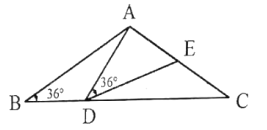
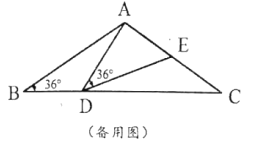
(1)若![]() ,证明:
,证明:![]() ;
;
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出![]() 的度数;若不可以,请说明理由.
的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点C.
交于点C.
(1)求直线![]() 的解析表达式;
的解析表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得
上存在异于点C的另一点P,使得![]() 与
与![]() 的面积相等,请求出点P的坐标.
的面积相等,请求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图在Rt△ABC中,斜边AB=5厘米,BC=![]() 厘米,AC=b厘米,
厘米,AC=b厘米,![]() >b,且
>b,且![]() 、b是方程
、b是方程![]() 的两根。
的两根。
⑴ 求![]() 和b的值;
和b的值;
⑵ ![]() 与
与![]() 开始时完全重合,然后让
开始时完全重合,然后让![]() 固定不动,将
固定不动,将![]() 以1厘米/秒的速度沿
以1厘米/秒的速度沿![]() 所在的直线向左移动。
所在的直线向左移动。
① 设x秒后![]() 与
与![]() 的重叠部分的面积为y平方厘米,
的重叠部分的面积为y平方厘米,
求y与x之间的函数关系式,并写出x的取值范围;
② 几秒后重叠部分的面积等于![]() 平方厘米?
平方厘米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com