
【题目】已知三点A(0,0),B(5,12),C(14,0),则△ABC内心的坐标为____.
【答案】(6,4).
【解析】
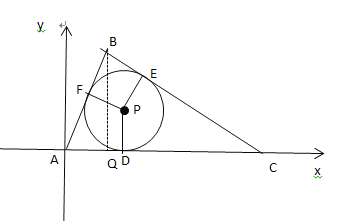
作BQ⊥AC于点Q,由题意可得BQ=12,根据勾股定理分别求出BC、AB的长,继而利用三角形面积,可得△OAB内切圆半径,过点P作PD⊥AC于D,PF⊥AB于F,PE⊥BC于E,设AD=AF=x,则CD=CE=14-x,BF=13-x,BE=BC-CE=15-(14-x)=1+x,由BF=BE可得13-x=1+x,解之求出x的值,从而得出点P的坐标,即可得出答案.
解:如图,过点B作BQ⊥AC于点Q,
则AQ=5,BQ=12,
∴AB=![]() ,CQ=AC-AQ=9,
,CQ=AC-AQ=9,
∴BC=![]()
设⊙P的半径为r,根据三角形的面积可得:r=![]()
过点P作PD⊥AC于D,PF⊥AB于F,PE⊥BC于E,
设AD=AF=x,则CD=CE=14-x,BF=13-x,
∴BE=BC-CE=15-(14-x)=1+x,
由BF=BE可得13-x=1+x,
解得:x=6,
∴点P的坐标为(6,4),
故答案为:(6,4).


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
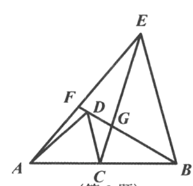
【题目】如图,在线段AB上有一点C,在AB的同侧作等腰△ACD和等腰△ECB,且AC=AD,EC=EB,∠DAC=∠CEB,直线BD与线段AE,线段CE分别交于点F,G.对于下列结论:①△DCG∽△BEG;②△ACE∽△DCB;③GF·GB=GC·GE;④若∠DAC=∠CEB=90°,则2AD2=DF·DG.其中正确的是( )
A.①②③④B.①②③C.①③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
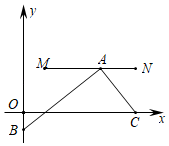
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
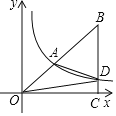
【题目】如图,反比例函数y=![]() (x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
(x>0)的图象经过Rt△BOC斜边上的中点A,与边BC交于点D,连接AD,则△ADB的面积为( )
A.12B.16C.20D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”为我们打开了交流、合作的大门,也为沿线各国在商贸等领域提供了更多的便捷,2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举办,据哈外贸商会发布消息,博览会期间,哈Paseka公司与重庆某国际贸易公司签订了供应蜂蜜合同:哈Paseka公司于2019年6月前分期分批向重庆某国际贸易公司供给优质蜂蜜共3000万件,该公司顺应新时代购物流,打算分线上和线下两种方式销售.
(1)若计划线上销售量不低于线下销售量的25%,求该公司计划在线下销售量最多为多少万件?
(2)该公司在12月上旬销售优质蜂蜜共240万件,且线上线下销售单件均为100元/件.12月中旬决定线上销售单价下调m%,线下销售单价不变,在这种情况下,12月中旬销售总量比上旬增加了m%,且中旬线上销售量占中旬总销量的![]() ,结果中旬销售总金额比上旬销售总金额提高了
,结果中旬销售总金额比上旬销售总金额提高了![]() m%.求m的值.
m%.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
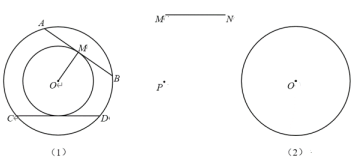
【题目】(1)如图,已知AB、CD是大圆⊙O的弦,AB=CD,M是AB的中点.连接OM,以O为圆心,OM为半径作小圆⊙O.判断CD与小圆⊙O的位置关系,并说明理由;
(2)已知⊙O,线段MN,P是⊙O外一点.求作射线PQ,使PQ被⊙O截得的弦长等于MN.
(不写作法,但保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
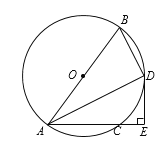
(1)求证:DE是⊙O的切线;
(2)若BD=3,AD=4,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点![]() ,
,![]() ,若点
,若点![]() 满足
满足![]() ,
,![]() ,那么称点
,那么称点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
例如:![]() ,
,![]() ,当点
,当点![]() 满是
满是![]() ,
,![]() 时,则点
时,则点![]() 是点
是点![]() ,
,![]() 的融合点,
的融合点,

(1)已知点![]() ,
,![]() ,
,![]() ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
①试确定![]() 与
与![]() 的关系式.
的关系式.
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m2?
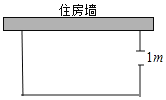
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com