
 ��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬����OABC�Ķ���A��$\sqrt{3}$��0����C��0��1������OAC=30�㣬����AOC��AC���۵á�APC��
��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬����OABC�Ķ���A��$\sqrt{3}$��0����C��0��1������OAC=30�㣬����AOC��AC���۵á�APC������ ��1�����÷��۱任�����ʵó�OA=AP=$\sqrt{3}$����PAC=��OAC=30�㣬���PAO=60�㣮��P��PQ��OA��Q����Rt��PAQ�����AQ��PQ�ij��������ɵõ���P�����ꣻ
��2����P��A�����������������ߵĽ���ʽ�У��õ�b��c��ֵ���Ӷ�ȷ�������ߵĽ���ʽ��Ȼ��C��������������ߵĽ���ʽ�н�����֤���ɣ�
��3�����������ߵĽ���ʽ�����D��E������꣬Ȼ�������������ǣ�
��DE��ƽ���ı��εĶԽ��ߣ�����CD��x�ᣬ��C��y���ϣ�����D��ֱ��CE��ƽ���ߣ���ô��ֱ����x��Ľ��㼴ΪM�㣬��N�㼴ΪC�㣬D��E�������Ѿ���ã����ƽ���ı����Լ�ƽ�Ƶ����ʼ��ɵõ���M�����꣬��C��������֪�����ɵõ�N������ꣻ
��DE��ƽ���ı��εıߣ�����A��x���ϣ���A��DE��ƽ���ߣ���y��Ľ��㼴ΪN�㣬��M�㼴ΪA�㣻����ƽ���ı����Լ�ƽ�Ƶ����ʼ��ɵõ�N������ꣻ
ͬ��������C��y���ϣ���CD��x�ᣬ��C��DE��ƽ���ߣ�Ҳ���ҵ�����������M��N�㣬�ⷨͬ�ϣ�
��� 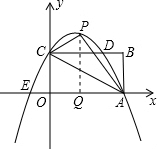 �⣺��1���߾���OABC�Ķ���A��$\sqrt{3}$��0����C��0��1����
�⣺��1���߾���OABC�Ķ���A��$\sqrt{3}$��0����C��0��1����
��OA=$\sqrt{3}$��OC=1����AOC=90�㣬
���OAC=30�㣮
�߽���AOC��AC���۵á�APC��
��OA=AP=$\sqrt{3}$����PAC=��OAC=30�㣬
���PAO=60�㣮
��P��PQ��OA��Q��
����Rt��PAQ�У���PAQ=60�㣬AP=$\sqrt{3}$��
��AQ=$\frac{1}{2}$AP=$\frac{\sqrt{3}}{2}$��PQ=$\sqrt{3}$AQ=$\frac{3}{2}$��
��OQ=OA-AQ=$\sqrt{3}$-$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$��
��P��$\frac{\sqrt{3}}{2}$��$\frac{3}{2}$����
��2����������y=-$\frac{4}{3}$x2+bx+c����P��$\frac{\sqrt{3}}{2}$��$\frac{3}{2}$����A��$\sqrt{3}$��0����
��$\left\{\begin{array}{l}{-\frac{4}{3}����\frac{\sqrt{3}}{2}��^{2}+\frac{\sqrt{3}}{2}b+c=\frac{3}{2}}\\{-\frac{4}{3}����\sqrt{3}��^{2}+\sqrt{3}b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=\sqrt{3}}\\{c=1}\end{array}\right.$��
��y=-$\frac{4}{3}$x2+$\sqrt{3}$x+1��
�ߵ�x=0ʱ��y=1��
��C��0��1���ڸ������ߵ�ͼ���ϣ�
��3������DE��ƽ���ı��εĶԽ��ߣ���C��y���ϣ�CD��x�ᣬ
����D��DM��CE��x����M�����ı���EMDCΪƽ���ı��Σ�EM=CD��
��y=1���������߽���ʽ�õ�D������Ϊ��$\frac{3\sqrt{3}}{4}$��1����
��y=0���������߽���ʽ�õ�E������Ϊ��-$\frac{\sqrt{3}}{4}$��0����
��EM=CD=$\frac{3\sqrt{3}}{4}$��
��M��$\frac{\sqrt{3}}{2}$��0����N�㼴ΪC�㣬�����ǣ�0��1����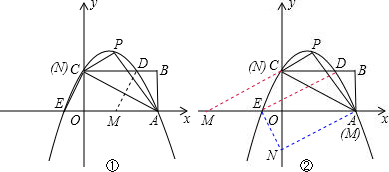
����DE��ƽ���ı��εıߣ�
����A��AN��DE��y����N���ı���DANE��ƽ���ı��Σ�AN��DE��AN=DE��
��D��$\frac{3\sqrt{3}}{4}$��1����E��-$\frac{\sqrt{3}}{4}$��0����
��D������ƽ��$\sqrt{3}$����λ��������ƽ��1����λ�õ���E��
���A��$\sqrt{3}$��0������ƽ��$\sqrt{3}$����λ��������ƽ��1����λ�õ���N��
��N��0��-1����M�㼴ΪA�㣬M��$\sqrt{3}$��0����
ͬ������C��CM��DE��y����N���ı���CMED��ƽ���ı��Σ�
��M��-$\sqrt{3}$��0����N��0��1����
���� �����Ƕ��κ����ۺ��⣬�����漰�����ε����ʡ�ͼ�εķ��۱任����ֱ�������Ρ����κ�������ʽ��ȷ����ƽ���ı��ε��ж������ʡ�ƽ�Ƶ����ʵ�֪ʶ���ۺ��Խ�ǿ���Ѷ����У��������ν�ϡ����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
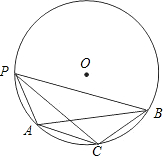 ��ͼ����PΪ��O��һ�㣬��AB=$\sqrt{3}$cm��PC�ǡ�APB��ƽ���ߣ���BAC=30�㣮
��ͼ����PΪ��O��һ�㣬��AB=$\sqrt{3}$cm��PC�ǡ�APB��ƽ���ߣ���BAC=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��M��N��AB�ϣ�AC=MP��AM=BN��BC=PN����֤��AC��MP��
��֪����ͼ��M��N��AB�ϣ�AC=MP��AM=BN��BC=PN����֤��AC��MP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l1��ֱ��l2��ֱ��l3���أ����ͬλ�ǡ�1���3��ȣ���ô�ڴ��ǡ�2���4��ȣ�ͬ���ڽǡ�2���3��������˵�����ɣ�
��ͼ��ֱ��l1��ֱ��l2��ֱ��l3���أ����ͬλ�ǡ�1���3��ȣ���ô�ڴ��ǡ�2���4��ȣ�ͬ���ڽǡ�2���3��������˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com