
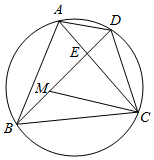
 如图,点D是等边三角形ABC外接圆上一点.M是BD上一点,且满足DM=DC,点E是AC与BD的交点.
如图,点D是等边三角形ABC外接圆上一点.M是BD上一点,且满足DM=DC,点E是AC与BD的交点.分析 (1)根据△ABC是正三角形,得出∠ADB=∠BDC=60°,再根据DM=DC,得到DM=CM=CD,最后根据∠ADB=∠DMC=60°,可判定CM∥AD;
(2)先根据△ADC≌△BMC,得出BD=3,再根据△ADE∽△CME,得到DE=$\frac{2}{3}$,ME=$\frac{4}{3}$,且AE=$\frac{1}{3}$AC,最后判定△ABE∽△DCE,得出$\frac{DC}{AB}$=$\frac{EC}{BE}$,即$\frac{2}{AB}$=$\frac{\frac{2}{3}AC}{1+\frac{4}{3}}$,求得AB=$\sqrt{7}$=BC,根据AE:CE=AD:CD=1:2,可得CE=$\frac{2}{3}$AC,最后根据△BCE的面积=$\frac{2}{3}$×△ABC的面积,求得S△BCE即可.
解答 解:(1)∵△ABC是正三角形,
∴$\widehat{AB}$=$\widehat{BC}$,
∴∠ADB=∠BDC=60°,
又∵DM=DC,
∴△CDM是等边三角形,即DM=CM=CD,
∴∠DMC=60°,
∴∠ADB=∠DMC=60°,
∴CM∥AD;
(2)∵∠DAC=∠DBC,∠BMC=∠ADC=120°,而AC=BC,
∴△ADC≌△BMC,
∴BM=AD=1,
∴BD=BM+MD=1+2=3,
由(1)可得,△ADE∽△CME,而AD=1,CM=2,
∴$\frac{AD}{CM}$=$\frac{AE}{CE}$=$\frac{DE}{ME}$=$\frac{1}{2}$,
又∵MD=2,
∴DE=$\frac{2}{3}$,ME=$\frac{4}{3}$,
∵$\frac{AE}{CE}$=$\frac{1}{2}$,且点E在线段AC上,
∴AE=$\frac{1}{3}$AC,
∵∠BAC=∠BDC=60°,∠ABD=∠ACD,
∴△ABE∽△DCE,
∴$\frac{DC}{AB}$=$\frac{EC}{BE}$,
∴$\frac{2}{AB}$=$\frac{\frac{2}{3}AC}{1+\frac{4}{3}}$,
又∵AB=AC,
∴AB2=7,即AB=$\sqrt{7}$=BC,
∵AD=1,CM=2,CM=CD,
∴AD:CD=1:2,
又∵∠ADE=∠CDE=60°,
∴BD平分∠ADC,
∴AE:CE=AD:CD=1:2,
∴CE=$\frac{2}{3}$AC,
∴△BCE的面积=$\frac{2}{3}$×△ABC的面积=$\frac{2}{3}$×$\frac{\sqrt{3}}{4}$×($\sqrt{7}$)2=$\frac{7}{6}\sqrt{3}$.
点评 本题主要考查了三角形的外接圆与外心、等边三角形的性质以及角平分线的性质的综合应用,解决问题的关键是根据全等三角形的性质以及相似三角形的性质进行求解.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
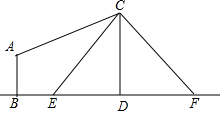 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com