
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 | |
| 学生奶 | 2 | 1 | 0 | 1 | 0 | 9 | 8 |
| 酸牛奶 | 70 | 70 | 80 | 75 | 85 | 80 | 100 |
| 原味奶 | 40 | 30 | 35 | 30 | 38 | 47 | 60 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 抛物线y=-(x-1)2+4与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为点D.
抛物线y=-(x-1)2+4与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为点D.| 10 |
| 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
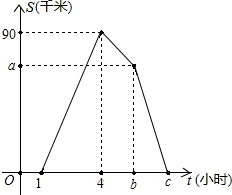 甲、乙两人同时从家乘车去书店,途中甲因故下车,改骑自行车前往书店(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达书店停留2小时后,以另一速度返回,2小时后与甲相遇.下图为甲、乙两人之间的距离S(千米)与行驶时间t(小时)之间的函数关系.
甲、乙两人同时从家乘车去书店,途中甲因故下车,改骑自行车前往书店(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达书店停留2小时后,以另一速度返回,2小时后与甲相遇.下图为甲、乙两人之间的距离S(千米)与行驶时间t(小时)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=8,sinB=
如图,在△ABC中,∠ACB=90°,AC=8,sinB=| 4 |
| 5 |
| PD |
| PQ |
| DE |
| QE |
查看答案和解析>>
科目:初中数学 来源: 题型:
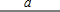

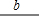
查看答案和解析>>
科目:初中数学 来源: 题型:
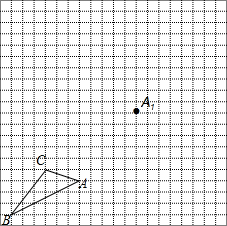 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com