
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
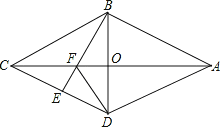
(1)证明:△CBF≌△CDF;
(2)若AC=2![]() ,BD=2,求四边形ABCD的周长;
,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.
【答案】(1)证明见解析;(2)8;(3)EB⊥CD,证明见解析.
【解析】
试题分析:(1)首先利用SSS定理证明△ABC≌△ADC可得∠BCA=∠DCA即可证明△CBF≌△CDF.
(2)由△ABC≌△ADC可知,△ABC与△ADC是轴对称图形,得出OB=OD,∠COB=∠COD=90°,因为OC=OA,所以AC与BD互相垂直平分,即可证得四边形ABCD是菱形,然后根据勾股定理全等AB长,进而求得四边形的面积.
(3)首先证明△BCF≌△DCF可得∠CBF=∠CDF,再根据BE⊥CD可得∠BEC=∠DEF=90°,进而得到∠EFD=∠BCD=∠BAD.
试题解析:(1)证明:在△ABC和△ADC中,
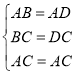 ,
,
∴△ABC≌△ADC(SSS),
∴∠BCA=∠DCA,
在△CBF和△CDF中,
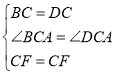 ,
,
∴△CBF≌△CDF(SAS),
(2)解:∵△ABC≌△ADC,
∴△ABC和△ADC是轴对称图形,
∴OB=OD,BD⊥AC,
∵OA=OC,
∴四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵AC=2![]() ,BD=2,
,BD=2,
∴OA=![]() ,OB=1,
,OB=1,
∴AB=![]() ,
,
∴四边形ABCD的周长=4AB=4×2=8.
(3)当EB⊥CD时,即E为过B且和CD垂直时垂线的垂足,∠EFD=∠BCD,
理由:∵四边形ABCD为菱形,
∴BC=CD,∠BCF=∠DCF,∠BCD=∠BAD,
∵△BCF≌△DCF,
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠BCD+∠CBF=90°,∠EFD+∠CDF=90°,
∴∠EFD=∠BAD.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
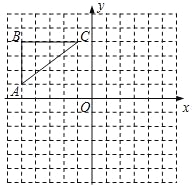
【题目】在正方形网格中,△ABC各顶点都在格点上,点A、C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2;
(3)点C1的坐标是 ;点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm. 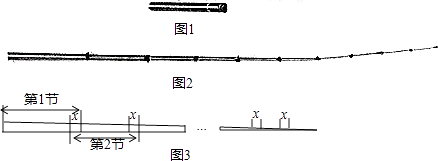
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月24日上午9时港珠澳大桥正式通车,它是东亚建设的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,整个大桥造价超过720亿元人民币,将72000000000用科学记数法表示为( )
A.7.2×1011B.7.2×1010C.0.72×1011D.72×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某函数满足当自变量x=-1时,函数的值y=2,且函数y的值始终随自变量x的增大而减小,写出一个满足条件的函数表达式____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com