
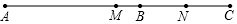 如图,点B在线段AC上,点M、N分别是AC、BC的中点.
如图,点B在线段AC上,点M、N分别是AC、BC的中点.分析 (1)先求得BC的长,再根据点M、N分别是AC、BC的中点,即可得到线段MN的长;
(2)先根据点M、N分别是AC、BC的中点,得到CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,再根据MN=CM-CN进行计算即可;
(3)分三种情况进行讨论:点B在线段AC上,点B在AC的延长线上,点B在CA的延长线上,分别根据点M、N分别是AC、BC的中点,依据线段的和差关系进行计算即可.
解答 解:(1)∵AC=15,BC=$\frac{2}{5}$AC,
∴BC=6,
又∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC=$\frac{15}{2}$,CN=$\frac{1}{2}$BC=3,
∴MN=CM-CN=$\frac{15}{2}$-3=$\frac{9}{2}$;
故答案为:$\frac{9}{2}$;
(2)∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CM-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$m;
(3)当点B在线段AC上时,
∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CM-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$(a-b);
当点B在AC的延长线上时,
∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CM+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$(a+b);
当点B在CA的延长线上时,
∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CN-CM=$\frac{1}{2}$BC-$\frac{1}{2}$AC=$\frac{1}{2}$(BC-AC)=$\frac{1}{2}$(b-a).
点评 本题主要考查了两点间的距离,解决问题的关键是运用分类讨论思想,依据线段的和差关系进行计算.


科目:初中数学 来源: 题型:解答题
 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°,点D在线段AB上,连接CD,∠ADC=60°,AD=2,过C作CE⊥CD,且CE=CD,连接DE,交BC于F.
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°,点D在线段AB上,连接CD,∠ADC=60°,AD=2,过C作CE⊥CD,且CE=CD,连接DE,交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{7}$-$\sqrt{7}$=2 | B. | $\sqrt{(a-b)^{2}}$=a-b | C. | 2$\sqrt{12}$×$\frac{1}{2}$$\sqrt{\frac{3}{4}}$=3 | D. | $\frac{\sqrt{18}-\sqrt{8}}{2}$=$\sqrt{9}$-$\sqrt{4}$=3-2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
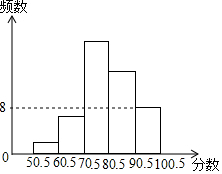 某班将全班同学一次知识竞赛成绩(整数)进行整理后,分成五组,绘成频数直方图,如图中从左到右的前四组的百分比分别是4%,12%,40%,28%,最后一组的频数是8,则该班有50名同学参赛.
某班将全班同学一次知识竞赛成绩(整数)进行整理后,分成五组,绘成频数直方图,如图中从左到右的前四组的百分比分别是4%,12%,40%,28%,最后一组的频数是8,则该班有50名同学参赛.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com