
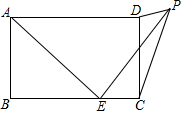
 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长3或$\frac{7+\sqrt{17}}{4}$. 分析 分两种情形讨论:①如图1中,当∠PDC=90°时.②如图2中,当∠DPC=90°时,作PF⊥BC于F,PH⊥CD于H,设BE=x.分别求解即可.
解答 解:①如图1中,当∠PDC=90°时,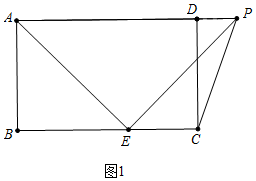
∵∠ADC=90°,
∴∠ADC+∠PDC=180°,
∴A、D、P共线,
∵EA=EP,∠AEP=90°,
∴∠EAP=45°,
∵∠BAD=90°,
∴∠BAE=45°,
∵∠B=90°
∴∠BAE=∠BEA=45°,
∴BE=AB=3.
②如图2中,当∠DPC=90°时,作PF⊥BC于F,PH⊥CD于H,设BE=x,
∵∠AEB+∠PEF=90°,∠AEB+∠BAE=90°,
∴∠BAE=∠PEF,
在△ABE和△EFP中,
$\left\{\begin{array}{l}{∠BAE=∠PEF}\\{∠B=∠F=90°}\\{AE=EP}\end{array}\right.$,
∴△ABE≌△EFP,
∴EF=AB=3,PF=HC=BE=x,
∴CF=3-(5-x)=x-2,
∵∠DPH+∠CPH+90°,∠CPH+∠PCH=90°,
∴∠DPH=∠PCH,
∵∠DHP=∠PHC,
∴△PHD∽△CHP,
∴PH2=DH•CH,
∴(x-2)2=x(3-x),
∴x=$\frac{7+\sqrt{17}}{4}$或$\frac{7-\sqrt{17}}{4}$(舍),
∴BE=$\frac{7+\sqrt{17}}{4}$,
综上所述,当△PDC是直角三角形时,BE的值为3或$\frac{7+\sqrt{17}}{4}$.
故答案为:3或$\frac{7+\sqrt{17}}{4}$.
点评 本题考查旋转变换、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线构造全等三角形或相似三角形解决问题,属于中考常考题型.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{a}$)2=a | B. | 若a>b(ab≠0),则$\frac{1}{a}$<$\frac{1}{b}$ | ||
| C. | |a|•|b|=|ab| | D. | 若m为整数,则(m+$\frac{1}{2}$)2+$\frac{7}{4}$是整数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 次数为2,项数为3 | B. | 因式分解的结果是(x-4)(x-6) | ||
| C. | 该代数式的值可能等于0 | D. | 该代数式的值可能小于-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
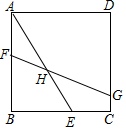 如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.
如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
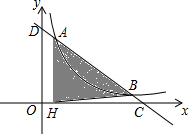 如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=1,则k的值为( )
如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=1,则k的值为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com