
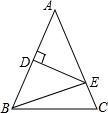
 如图,在△ABC中,AC=12cm,ED垂直平分AB,如果△EBC的周长是20cm,那么BC的长度为8cm.
如图,在△ABC中,AC=12cm,ED垂直平分AB,如果△EBC的周长是20cm,那么BC的长度为8cm.  同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
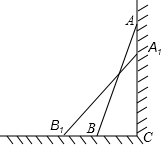 小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com