
分析 利用完全平方公式和通分等方法将原分式化简成$\frac{m}{m+1}$,并找出m的取值范围,随便选取一个使原分式有意义的数,代入化简后的分式中即可得出结论.
解答 解:原式=$\frac{{m}^{2}}{(m+1)^{2}}$÷$\frac{m+1-1}{m+1}$,
=$\frac{{m}^{2}}{(m+1)^{2}}$•$\frac{m+1}{m}$,
=$\frac{m}{m+1}$.
∵(m+1)•m≠0,
∴m≠-1且m≠0.
取m=3,
原式=$\frac{m}{m+1}$=$\frac{3}{4}$.
点评 本题考查了分式的化简求值,解题的关键是将原分式化简成$\frac{m}{m+1}$,并求出m的取值范围.本题属于基础题,难度不大,解决该题型题目时,先对原分式进行化简,再选取合适的数值代入化简后的分式(或整式)中求出结果即可.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
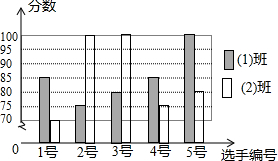 为了弘扬“中国梦”,某校初三(1)班和初三(2)班各5名同学参加以“诚信•友善”为主题的演讲比赛活动,根据他们的得分情况绘制如下的统计图:
为了弘扬“中国梦”,某校初三(1)班和初三(2)班各5名同学参加以“诚信•友善”为主题的演讲比赛活动,根据他们的得分情况绘制如下的统计图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com