
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).


【答案】![]()
【解析】(1)过点B作BM∥FG交CD于M ,构造三角形,证△BCM≌△CDE,可得; CE=BM=FG;(2) 过点B作BM∥FG交CD于M , 连接MO,由(1)证BC=BO,再证MC=MO=MG=ED,又AD=3DE,所以![]() ;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
又BM=CE=![]() ,再根据面积公式得OC=2×
,再根据面积公式得OC=2×![]() .
.
(1)过点B作BM∥FG交CD于M ,
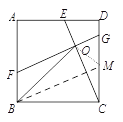
易证四边形FBMG为平行四边形
∴FG=BM,
由BC=CD;∠BCM=∠CDE;∠MBC=∠ECD
可证△BCM≌△CDE,
∴CE=BM=FG;
(2)过点B作BM∥FG交CD于M ,
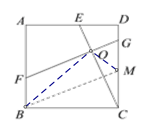
由(1)知△BCM≌△CDE,又∠OBC=2∠DCE ,
MC=ED,∠MBC=∠DCE=∠MBO,
由BM∥FG得MB⊥CE,
∴∠BOC=∠BCO,
∴BC=BO,连接MO,
∴BM垂直平分OC,
∴MC=MO,
又∵∠GOM=∠BMO=∠BMC=∠OGM
∴MC=MO=MG=ED,
又AD=3DE,
∴![]() ;
;
(3)∵AD=3,
∴由(1)(2)可得
DE=OM=1,BO=AD=3,∴BM=CE=![]() ,
,
OC=2×![]() =2×
=2×![]() =
= ![]() ,
, ![]()
![]()
∴OE=CE-CO=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地。假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等,)又顺水航行返回万州,若该轮船从万州出发后所用时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能反映y与x之间函数关系的图象大致是【 】
A. B.
B.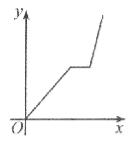 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2(m+1)x+m(m+2)
(1)求证:无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值.
(2)若该函数图象的对称轴为直线x=2,试求二次函数的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当![]() 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当![]() 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l:![]() 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线![]() 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:![]() 交线段AB于点D。
交线段AB于点D。
如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若![]() ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;
如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。
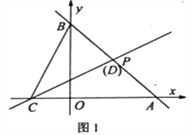

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的费用;
(2)若有50名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10(n是大于0的整数)个图形需要黑色棋子的个数是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别从
,甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲速每小时
两地同时出发,甲速每小时![]() 千米,乙速每小时
千米,乙速每小时![]() 千米,请按下列要求列方程解题:
千米,请按下列要求列方程解题:
![]() 若同时出发,相向而行,多少小时相遇?
若同时出发,相向而行,多少小时相遇?
![]() 若同时出发,相向而行,多长时间后两车相距
若同时出发,相向而行,多长时间后两车相距![]() ?
?
![]() 若同时出发,同向而行,多长时间后两车相距
若同时出发,同向而行,多长时间后两车相距![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com